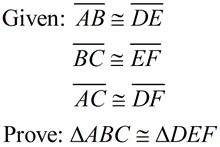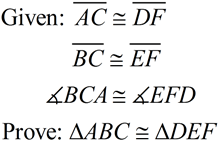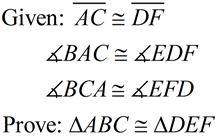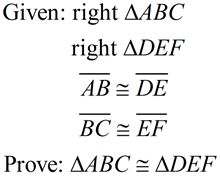|
|
Two figures are congruent if and only if there exists one, or more, rigid transformations which will map one figure onto the other. |
|
The following sections will verify that each of the accepted methods of proving triangles congruent (SSS, SAS, ASA, AAS, and HL) follows from the definition (shown above) of congruence in terms of rigid transformations.
Note: The locations of the triangles in the "statement of the problem" show the triangles being parallel.
This may not always be the case.
Reference (1.) in the solution will mention other possible locations
of the given triangles
in relation to one another.
Given three sets of congruent sides, we seek a sequence of rigid transformations that will map ΔABC onto ΔDEF proving the triangles congruent.
|
 |
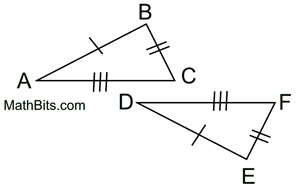
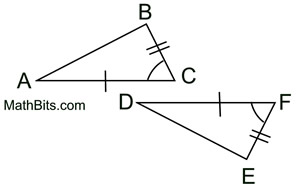
1. Given 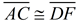 , there is a rigid transformation that will map 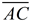 onto 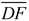 . A translation moving to the right and down assuming 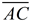 || 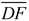 . If not parallel, a rotation after translating point A to point D will be needed. Should B' and E be on the same side of 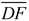 , reflect Δ A'B'C' over 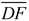 , so B' and E are on opposite sides of 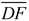 . |
|
2.
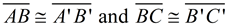 since translations (and rotations) are rigid transformations preserving length.
|
3. It is given that 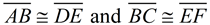 . By the transitive property of congruence, 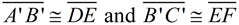 .
|
|
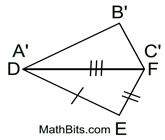
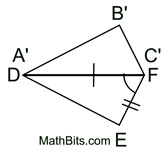
4. Draw a segment from B' to E.
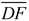 must be the perpendicular bisector of 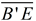 , because 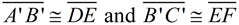 . Points along a perpendicular bisector of a segment are equidistant from the endpoints of the segment. Thus, 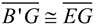 . (B and E are the same distance from G.)
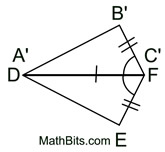
5. Points A' and C' lie on 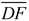 coinciding with points D and F. coinciding with points D and F.
Point B' can now be mapped onto E by a reflection in 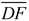 . .
6. ΔABC has been mapped onto ΔDEF through a series of rigid transformations and 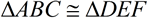 . .
|
|
Given two sets of sides and the included angles congruent, we seek a sequence of rigid transformations that will map ΔABC onto ΔDEF proving the triangles congruent.
|
 |
1. Given 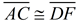 , there is a rigid transformation that will map 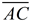 onto 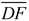 . A translation moving to the right and down assuming 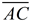 || 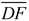 . If not parallel, a rotation after translating point A to point D will be needed. Should B' and E be on the same side of 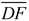 , reflect Δ A'B'C' over 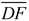 , so B' and E are on opposite sides of 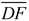 . |
|
2. 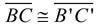 since translations (and rotations) are rigid transformations preserving length.
|
3. 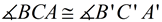 since translations (and rotations) preserve angle measure.
|
4. It is given that 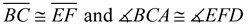 . Therefore, 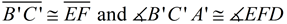 by the transitive property of congruence.
5. 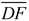 must be the bisector of must be the bisector of 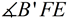 as an angle bisector forms two congruent angles. as an angle bisector forms two congruent angles.
|
|
6. Map point B' onto point E by a reflection in 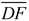 . Reflections will preserve angle measure so . Reflections will preserve angle measure so 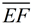 will coincide with will coincide with 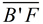 . Since . Since 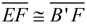 , B' and E will be the same length from point F, thus causing E to coincide with B'. , B' and E will be the same length from point F, thus causing E to coincide with B'.
7. ΔABC has been mapped onto ΔDEF through a series of rigid transformations and 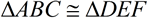 . . |
|
Given two sets of angles and the included sides congruent, we seek a sequence of rigid transformations that will map ΔABC onto ΔDEF proving the triangles congruent.
|

If we verify ASA, we have also verified AAS. If two sets of angles of two triangles are congruent, their third angles are also congruent. So any AAS situation can quickly become an ASA situation. |
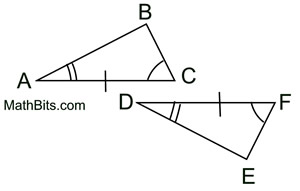
1. Given 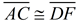 , there is a rigid transformation that will map 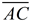 onto 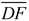 . A translation moving to the right and down assuming 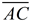 || 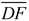 . If not parallel, a rotation after translating point A to point D will be needed. Should B' and E be on the same side of 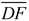 , reflect Δ A'B'C' over 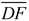 , so B' and E are on opposite sides of 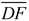 . |
|
2. 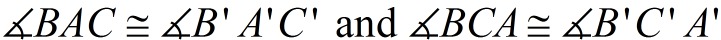 since translations (and rotations) are rigid transformations preserving angle measure.
|
|
|
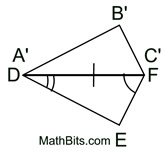
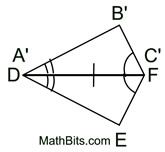
5. After a reflection in 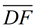 of ΔA'B'C' onto ΔDEF, point B' will coincide with point E. Points D (A') and F (C ') will not move during the reflection. Ray of ΔA'B'C' onto ΔDEF, point B' will coincide with point E. Points D (A') and F (C ') will not move during the reflection. Ray 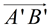 will coincide with ray will coincide with ray 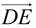 , and ray , and ray 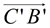 will coincide with ray will coincide with ray 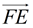 because reflections preserve angles, and rays coming from the same point at the same angle will coincide. Now, rays because reflections preserve angles, and rays coming from the same point at the same angle will coincide. Now, rays 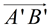 and and 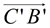 can only intersect at point B', and rays can only intersect at point B', and rays 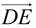 and and 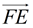 can only intersect at point E. Since the rays coincide, their intersection points, B' and E, will also coincide. can only intersect at point E. Since the rays coincide, their intersection points, B' and E, will also coincide.
6. ΔABC has been mapped onto ΔDEF through a series of rigid transformations and 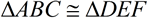 . . |
|
Given the corresponding hypotenuses and legs of two right triangles congruent, we seek a sequence of rigid transformations that will map right ΔABC onto right ΔDEF proving the right triangles congruent.
|
|
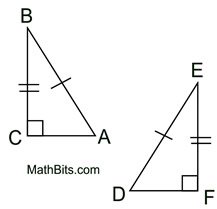
1. Given 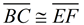 , there is a rigid transformation that will map 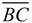 onto 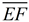 . A translation moving to the right and down assuming parallel segments. If not parallel, a rotation after translating point B to point E will be needed. Should A' and D be on the same side of 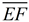 , reflect Δ A'B'C' over 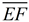 , so A' and D are on opposite sides of 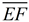 . |
|
2. 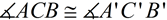 since translations (and rotations) are rigid transformations preserving angle measure.
|
3. 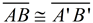 since translations (and rotations) preserve length.
|
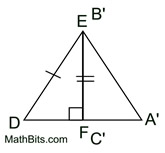
4. It is given that 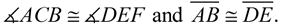 Therefore, 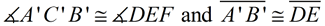 by the transitive property of congruence.
5. 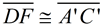 by the Pythagorean Theorem. by the Pythagorean Theorem.
|
|
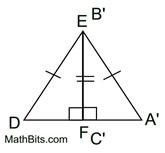
6. Map point A' onto point D by a reflection in 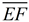 . . 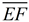 is the perpendicular bisector of is the perpendicular bisector of 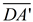 and all points lying on the perpendicular bisector of a segment are equidistant from the endpoint of the segment. So and all points lying on the perpendicular bisector of a segment are equidistant from the endpoint of the segment. So 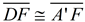 and under a reflection A' will coincide with D. and under a reflection A' will coincide with D.
7. Right ΔABC has been mapped onto right ΔDEF through a series of rigid transformations and 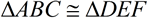 . . |
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|