|
Directions: Read each question carefully. Choose the best answer.
1. |
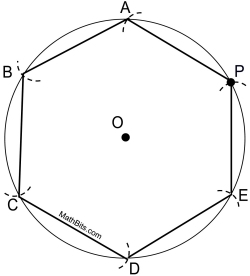
In the diagram of a construction at the right,
a) what is the measure of ∠AOB?
b) what is the measure of ∠BCD?
|
 |
|
2. |
In the construction of a square inscribed in a circle, which step follows drawing the circle?
Choose:
|
|
|
3. |
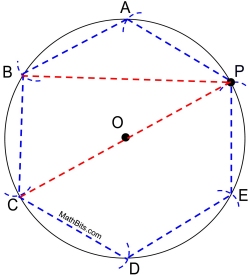
The diagram at the right shows the construction of a regular hexagon inscribed in a circle. Two additional segments have been added (red).
What type of triangle is ΔPBC ?
|
 |
|
4. |
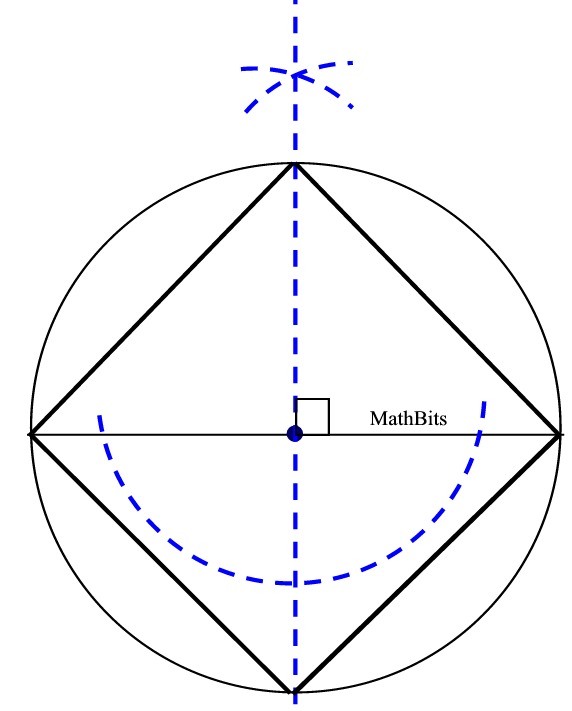
A square is inscribed in a circle, as shown, using only the construction "perpendicular at a point on a line", with the point being the circle's center and the line being the diameter.
Normally, this construction uses a "perpendicular bisector" of the diameter, thus doing both "perpendicularity" and "bisection".
Why is this method also acceptable?
|
 |
| |
|
|
5. |
The construction shown below starts with circle O. Circles Q and P each have the same radius as circle O, and pass through point O. |
| |
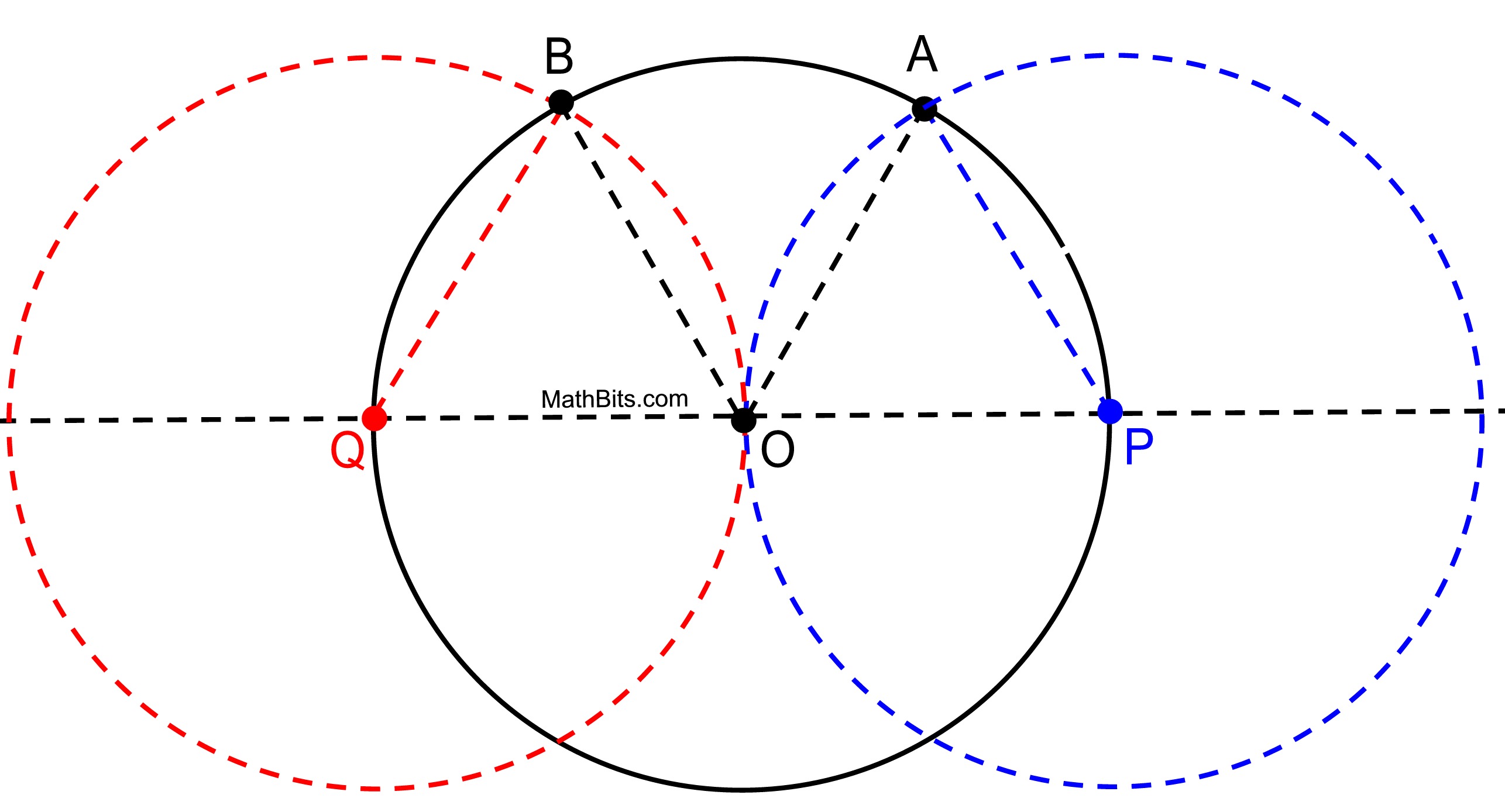
a) What is the measure of ∠OAP ?
Choose:
b) Which of the following statements is NOT true regarding this construction as shown?
Choose:
c) This technique is a sufficient method for constructing a regular hexagon inscribed in a circle, with the stipulation that ...
Choose:
|
|
6. |
When constructing a tangent to a circle at a point ON the circle, which construction is used?
Choose:
|
|
|
7. |
You are given the task of finding the center of a circle in which the center in not indicated. The theorem "In a circle, the perpendicular bisector of a chord passes through the center of the circle." is used for this construction.
Which of the following choices will not be an option for this construction?
|
|
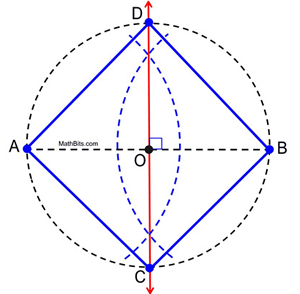
8. |
In the construction shown at the right, a) what is the measure of ∠ ADB?
b) What is the measure of ∠ABC?
c) What is the measure of the arc intercepted by two adjacent sides of the square?
Choose:
|
 |
|
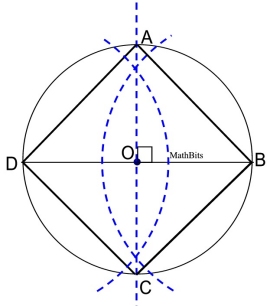
9. |
Regarding the construction shown at the right, what is the measure of ∠ AOC?
|
 |
|
10. |
When inscribing a square in a circle, using the method shown at the right, you are relying on which fact about squares?
|
|
|
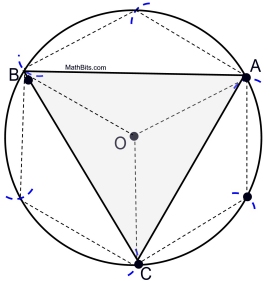
11. |
When preparing the construction of a regular hexagon inscribed in a circle, which of the following statements is NOT true?
|
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|