|
Let's quickly review what we already know about reflections in a line
and how the pre-image and image are positioned in relation to one another.
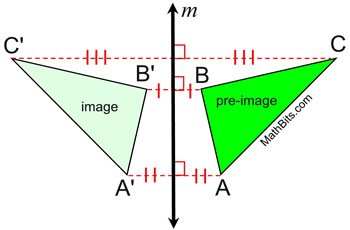
 An object and its reflection in a line have the same shape and size, but the figures face in opposite directions, appearing as mirror images.
The reflection line, m, is the perpendicular bisector of the segments joining each point to its image.
The existence of the perpendicular bisector will be the reflection's connection to constructions. Let's see how we can put it to work. |
If you need additional information on reflections,
go to the lesson on Line Reflections.
|
 Given a figure and line of reflection, construct the reflected image.
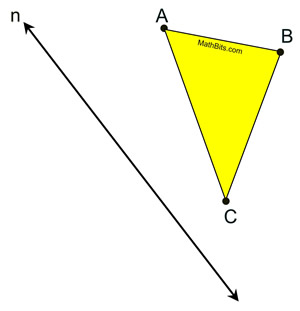
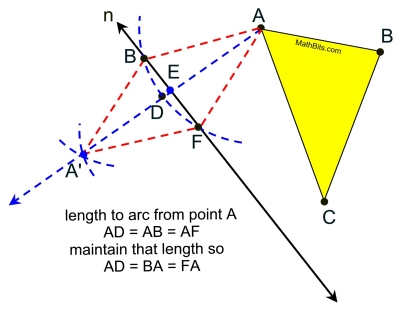
Given: ΔABC and reflection line n in the same plane.
Task: Construct the reflected image of ΔABC and label it ΔA'B'C'
 |
Choose a starting vertex (such as A). Construct a perpendicular from A to the line of reflection. Measure the length from A to the intersection point. Copy this length on the perpendicular bisector starting at the intersection point to find A'.
You have located ONE vertex of the image.
 |
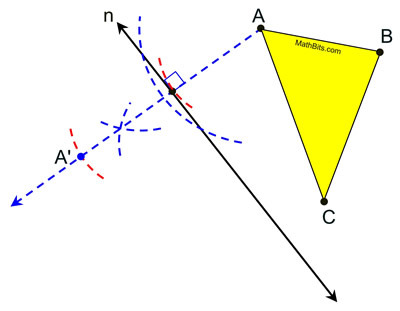| In this construction, the compass was set to draw the first arc from point A. The compass length was then changed to draw the second set of arcs (shown just above A' ). The length from A to the reflection line was then measured and copied to locate A'. |
After repeating this process for each of the three vertices, you will have the vertices of the image ΔA'B'C'. Done.
The order in which you repeat this process is of no importance. |
 |
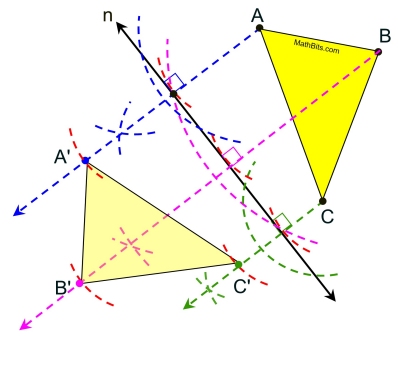| Addendum: If you DO NOT CHANGE the compass length after making the arc from point A, you can save yourself a step. If the second set of crossing arcs are created with that same length, the intersection point will be the image point, A'. Copying length AE is not needed. |
If AD is maintained as the compass length, then AD = BA' = FA'.
The "crossing arcs" now land exactly on the image A', making it unnecessary to measure and copy length AE.
Why does NOT changing the arc length give the image point immediately?
The figure ABA'F is a rhombus.
It has 4 congruent sides and diagonals that are perpendicular and bisect each other.
ΔABE, ΔAFE, ΔA'FE, and ΔA'BE are congruent triangles with AE = A'E. Done. |
 |
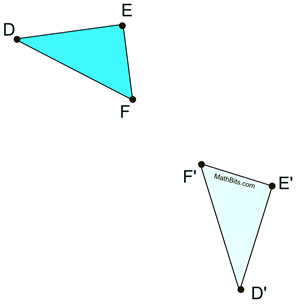
Given a figure and its reflection, construct the line of reflection.
Given: ΔD'E'F' is the reflection of ΔDEF
in some line in the same plane.
Task: Construct the line of reflection
 |
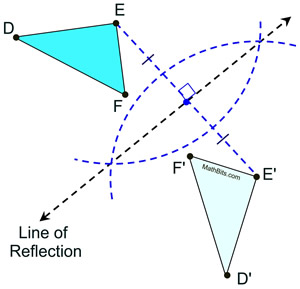
Connect any vertex of ΔDEF to its image
(such as E to E'). Construct the perpendicular bisector of the segment formed. Done.
 |
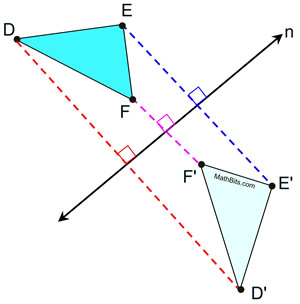
This example chose to connect E to E'. You could, however, have chosen to connect D to D' or F to F' for your construction.
It is sufficient to choose only one set of corresponding points to get the line of reflection. You need not bisect all three connected segments, unless you want to test the accuracy of your construction. |
 |
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
