|
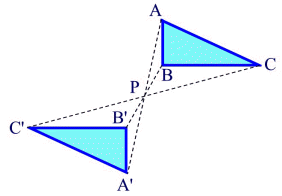
Let's quickly review what we already know about reflections in a point
and how the pre-image and image are positioned in relation to one another.
 An object and its reflection in a point have the same shape and size. The pre-image has been rotated 180º, and center point, P, is the midpoint of the segments connecting each set of vertices.
The existence of the midpoint of a line segment will be the point reflection's connection to constructions. Let's see how we can put it to work. |
|

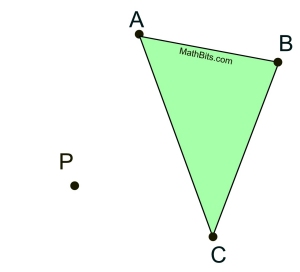
 Given a figure & a point of reflection, construct the reflected image. Given a figure & a point of reflection, construct the reflected image.
Given: ΔABC and reflection point P in the same plane.
Task: Construct the point reflection of ΔABC and label it ΔA'B'C'
|
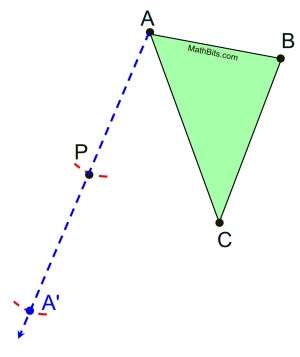
Choose a starting vertex (such as A). Draw a straight line from A through P (extend the line beyond P).
Remember, P is the midpoint of the segment connecting the corresponding vertices.
Measure the length from A to P. Copy this length starting at P and mark off length on the line.
P is now the midpoint and you have located ONE vertex, A', of the image.
|
 This construction is also the construction for a rotation of 180º This construction is also the construction for a rotation of 180º
about a point. |
After repeating this process from each of the three vertices, you will have the vertices of the image ΔA'B'C'.
You have made P the midpoint of all three segments connecting the corresponding vertices.
Done.
The order in which you repeat this process is of no importance. |
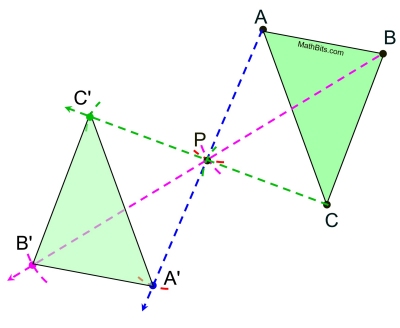 |

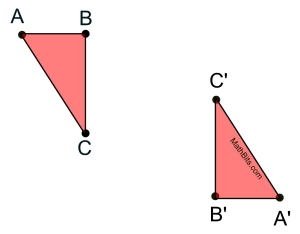
 Given a figure and its point reflection, construct the center point. Given a figure and its point reflection, construct the center point.
Given: ΔABC and its point reflection ΔA'B'C' through oint P in the same plane.
Task: Construct the center point P.
|
Choose a starting vertex (such as B). Draw a line segment connecting B to B'.
Remember, P is the midpoint of the segment connecting the corresponding vertices.
Bisect the segment from B to B' to find the midpoint, P. Done.
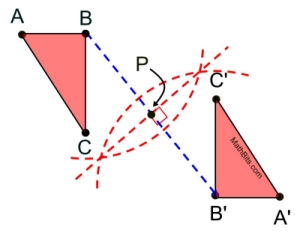
There is no need to repeat this process for the other vertices, other than to verify your construction.
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|