|
A piece of string can be an impressive geometric construction tool. When held down at one end, a string can be used to create a circle. When tightly stretched, a string can act as a straightedge.
The constructions below are samples of constructions using string. The steps to perform these constructions are the same as those followed when using a compass and straightedge.
Before beginning the construction, secure a piece of string to your writing utensil. To secure one end of the string to the paper, use a push-pin (as shown on this page), or secure the end by holding it in place with your free hand. Practice before you begin to see the method that works the best for you.
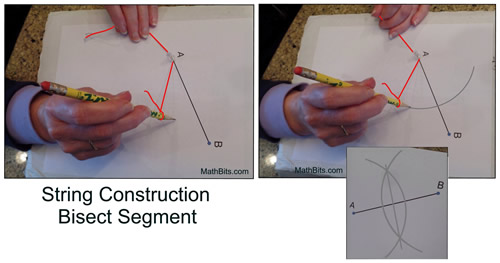
Construct a bisector of a segment. |
Steps: Bisect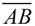 
1) Secure push-pin at A. Set string length more than half of AB. Swing arc.
2) Move push-pin to B. With same length of string swing another arc.
3) Draw line through points where arcs intersect.
4) This line is the bisector of the segment. |
|
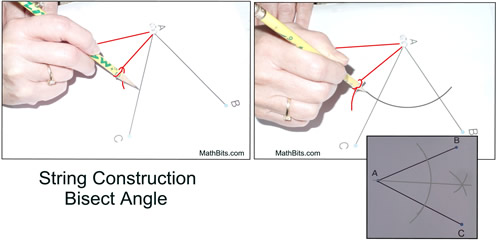
Construct an angle bisector. |
Steps: Bisect ∠BAC
1) Secure push-pin at A. Set string length. Swing arc.
2) Move push-pin to arc's intersection on one ray. Swing arc in interior.
3) Repeat from other ray with same length string.
4) Connect A to intersection in interior of angle. |
|
Construct a perpendicular from a point not on a line. |
Steps:
1) Secure push-pin at P. Set string length past line. Swing arc.
2) Move push-pin to arc's intersection on line. Swing arc below line.
3) Repeat from other intersection with line with same length string.
4) Connect intersection of arcs to P. |
|
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
