|
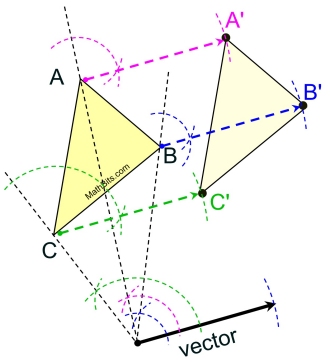
Let's quickly review what we already know about translations in a plane
and how the pre-image and image are positioned in relation to one another.
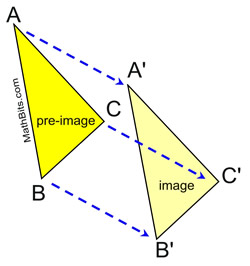
The blue dotted arrow signifies the vector, which determines the direction and distance to move the yellow triangle.
The dotted arrows are of equal length and parallel.
If you need additional information on translations, go to the lesson on Translations.
|
 A translation of an object is a "slide" of the object with a pre-determined distance and direction. The figure retains its same size and shape. The pre-image and image are congruent and point in the same direction. A translation of an object is a "slide" of the object with a pre-determined distance and direction. The figure retains its same size and shape. The pre-image and image are congruent and point in the same direction. The pre-determined direction and distance to move the object can be represented by a vector.
The fact that the segments connecting the
corresponding vertices are parallel and of
equal distances in the same directions (by vector),
will be the translation's connection to constructions.
Let's see how we can put it to work.
|

 Method 1: Given a vector and a figure, construct the translation. Method 1: Given a vector and a figure, construct the translation.
(This method is the most widely used method, as it uses the information discussed above: parallel lines and length).
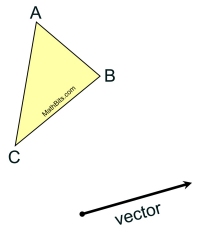
Given: ΔABC and a vector that will determine the translation.
Task: Construct the translation of ΔABC and label it ΔA'B'C'. |
|
First, examine the given diagram.
The vector points the direction of the translation, and the length of the vector will be the distance of the translation.
We can see that the translation will be to the right of the figure (since the vector points right), and will be slightly higher up than the figure (since the vector arrow points slightly upward).
|
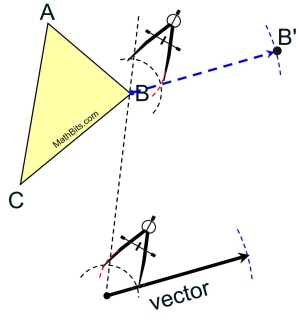
The compasses are showing the "span" length across the arc. |
The task is to construct a line parallel to the vector through each vertex of the triangle.
(You know this parallel line construction.)
Let's start with vertex B.
Start by drawing a transversal.
Draw a line through B and the starting point of the vector to form a transversal.
•
Construct an arc at angle formed with vector.
• Copy arc at point B.
• Measure "span" of arc at vector with compass.
• Transfer "span" to point B.
• Connect point B to span-arc crossing.
This is the parallel line.
Now, measure length of vector, making an
arc to show you measured the vector.
Mark this length on the new parallel line.
|
Observe how the 3 transversals
meet at the start of the vector. |
Repeat this process for the remaining two vertices of the triangle, A and C, to locate all three vertices of the image.
Connect the points A', B', and C' and the
translation is complete.
The secret to doing translation constructions,
is to
draw the transversals
that will go through each of the vertices and the starting point of the vector.
Then, IGNORE the SIDES of the triangles.
Pretend the triangles disappear except for their vertex points.
 Remember, you are working with the vector, Remember, you are working with the vector,
the vertex points, and the transversals only!
|

Let's try another example with Method 1:
 Method 1: Method 1: Given a vector and a figure, construct the translation.
Given: Parallelogram ABCD and a vector that has translated point B to B'.
Task: Construct the translation of ABCD and label it A'B'C'D'. |
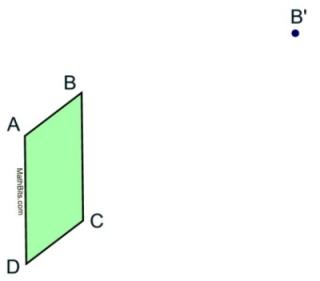
|
In this problem, instead of showing us the vector, we were given the location of a point (B') which is a result of the translation vector,
The vector representing the translation in this problem has length BB' and has direction to the right and slightly higher up.
|
Construct the parallel lines starting with the transversals and the vector. Copy the corresponding angles.
Use the compass to measure the length of the vector
and mark it on your parallel lines.
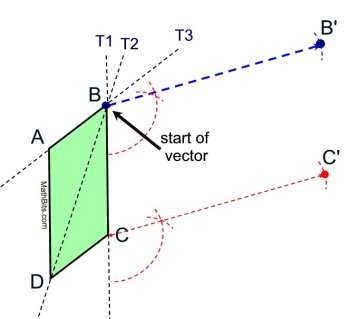
|
Our first step will be to draw the vector connecting B to B'. This will be the segment to which the other representations of the vector will be parallel and congruent.
Point B' has been located for us.
Again, the secret to doing translation constructions is to draw the transversals that pass through each vertex and the start of the vector (which in this problem is point B).
Draw tranversals: T1, T2, T3.
through the start of the vector (not the arrow) and the vertices of the parallelogram.
Now, IGNORE the SIDES of the parallelogram. You are working only with the vector, the vertex points, and the transversals.
Yes, two of the transversals passes through sides of the parallelogram. Think of them as "transversals", not as "sides". |
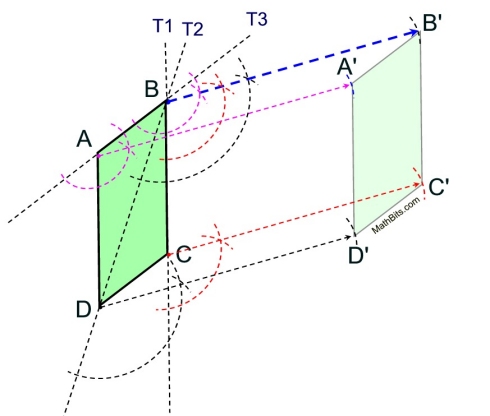
Look at how the parallel lines were constructed based upon the vector and the transversals. Ignore the sides of the parallelogram. Use the transversals.
Otherwise, the diagram can get horribly confusing.
|

Let's take a look at a different method for constructing translations.
 Method 2: Utilize the formation of a parallelogram to translate figure. Method 2: Utilize the formation of a parallelogram to translate figure.
Given: ΔABC and a vector that will determine the translation.
Task: Construct the translation of ΔABC and label it ΔA'B'C'. |
|
|
This is the same triangle and vector
used in the first example.
In this method, the concept of parallel lines will be introduced through the formation of a parallelogram.
|
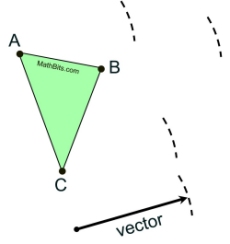 |
First, let's establish the "distance" of the translation from each vertex.
With your compass, measure the length of the vector. Place an arc at the end of the vector to show it was measured.
Now, with this distance, place your compass point on each of the triangle vertices and mark off the distance. Try to place your arc in the approximate location of where the image points will be (remember: to the right of the figure and slightly above). |
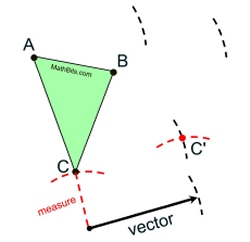 |
Now, measure the distance from the start of the vector (the dot) to point C. Mark this length.
Move compass point to the end of the vector (the arrowhead) and mark off this same length, so it intersects the existing arc.
This is the location of C' |
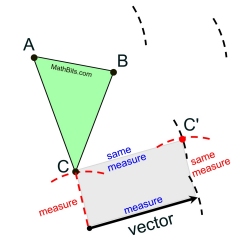 |
How do we know this is the location of C' ?
With the copies of the distances made,
a parallelogram (with opposite sides congruent)
has been formed.
A quadrilateral with 2 set of opposite sides
congruent is a parallelogram.
Being a parallelogram guarantees that the vector from C to C' points in the same direction and has the same length as the given vector. |
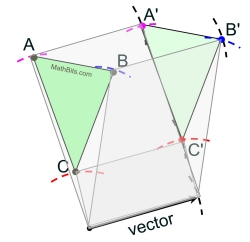 |
Repeat this process for the remaining two vertices of the triangle, A and B.
Connect the points A', B', and C' and the
translation is complete.
This diagram shows the parallelograms at work. The actual parallelograms are NOT part of the final construction. |
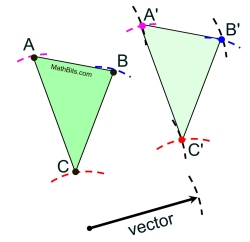 |
Finished Construction |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|














