Copy an Angle MathBitsNotebook.com Topical Outline | Geometry Outline | MathBits' Teacher Resources Terms of Use   Contact Person: Donna Roberts

Remember -- use your compass and straightedge only!

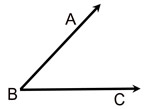
A construction associated with "copying an angle" requires that you have a "place" to begin your copy. It is customary to draw a straight line upon which you then produce your copy. Such a line is called a "reference line".

Given: ∠ABC Construct: an angle congruent to ∠ABC. (make a copy of the angle)

STEPS:
1. Using a straightedge, draw a reference line, if one is not provided.

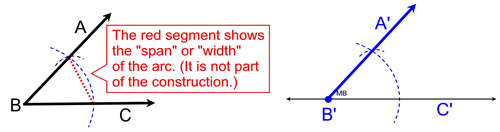
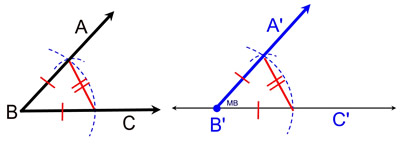
2. Place a dot (starting point) on the reference line.

3. Place the point of the compass on the vertex of the given angle, ∠ABC (vertex at point B).

4. Stretch the compass to any length that will stay "on" the angle.

5. Swing an arc so the pencil will cross BOTH sides (rays) of the angle.

6. Without changing the size of the compass, place the compass point on the starting point (dot) on the reference line and swing an arc that will intersect the reference line and go above the reference line.

7. Go back to the given angle ∠ABC and, using your compass, measure the span (width) of the arc from where it crosses one side of the angle to where it crosses the other side of the angle. (Place a small arc to show you measured this distance.)

8. Using this width, place the compass point on the reference line where the previous arc crosses the reference line and mark off this new width on your new arc.

9. Connect this new intersection point to the starting point (dot) on your reference line.

10. Label your copy.

Proof of Construction: When your construction is finished, draw line segments and , which represent the measured distances DE = FG. We know the lengths BD = BE = B'F = B'G since these are radii of the same (or congruent) circles. Now, we have two triangles, ΔBDE and ΔB'FG, that have 3 sets of congruent (equal) sides. Since the triangles are congruent by SSS and any leftover corresponding parts will also be congruent (by CPCTC), we know that ∠DBC (also named ∠ABC) is congruent to ∠FB'G (also named ∠A'B'C').