Construct: Tangent to a Circle at a Point ON the Circle MathBitsNotebook.com Topical Outline | Geometry Outline | MathBits' Teacher Resources Terms of Use   Contact Person: Donna Roberts

Remember -- use your compass and straightedge only!

This construction is an easy one if you remember that in a circle, a radius drawn to the point of tangency is perpendicular to the tangent. Use the construction: construct a perpendicular to a line from a point on the line. This construction is simply a variation of a construction you already know how to draw.

Given: Circle O Construct: a tangent to circle at a point on the circle STEPS: 1. If a point on the circle is not given, draw any radius and label P. If a point is already given on the circle, connect the point to the center of the circle to form a radius. 2. Extend the radius past the circle. 3. Construct a perpendicular to the radius line at point P.

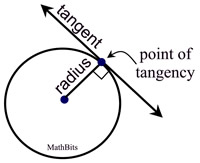
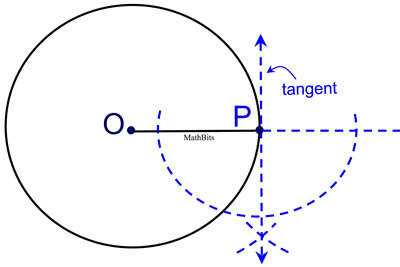
Proof of Construction: By construction, the line through point P is perpendicular to the line through O and P. The line through P is tangent to circle O, as verified by the theorem:
"A line perpendicular to the radius of a circle (at its point on the circumference) is a tangent to the circle at that point."