Equilateral Triangle MathBitsNotebook.com Topical Outline | Geometry Outline | MathBits' Teacher Resources Terms of Use   Contact Person: Donna Roberts

Remember -- use your compass and straightedge only!

We will be looking at THREE different constructions of an equilateral triangle. The first will be to construct an equilateral triangle given the length of one side (you have seen this construction), and the other two will be to construct an equilateral triangle inscribed in a circle.

Given: the length of one side of the triangle Construct: an equilateral triangle

STEPS:
1. Place your compass point on A and measure the distance to point B. Swing an arc of this size above (or below) the segment.

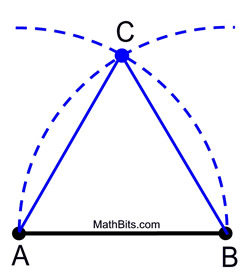
2. Without changing the span on the compass, place the compass point on B and swing the same arc, intersecting with the first arc.

3. Label the point of intersection as the third vertex of the equilateral triangle.

See the full circles at work.

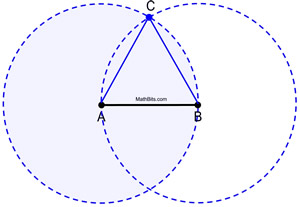
Proof of Construction: Circle A is congruent to circle B, since they were each formed using the same radius length, AB. Since AB and AC are lengths of radii of circle A, they are equal to one another. Similarly, AB and BC are radii of circle B, and are equal to one another. Therefore, AB = AC = BC by substitution (or transitive property). Since congruent segments have equal lengths, and ΔABC is equilateral (having three congruent sides).

STEPS:
1. Place your compass point on the paper and draw a circle. (Keep this compass span!)

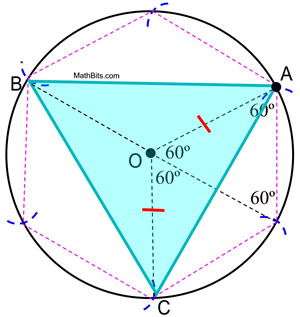
2. Place a dot, labeled A, anywhere on the circumference of the circle to act as a starting point.

3. Without changing the span on the compass, place the compass point on A and swing a small arc crossing the circumference of the circle.

4. Without changing the span on the compass, move the compass point to the intersection of the previous arc and the circumference and make another small arc on the circumference of the circle.

5. Keep repeating this process of "stepping" around the circle until you return to point A.

6. Starting at A, connect every other arc on the circle to form the equilateral triangle.

Refer to the proof of an inscribed regular hexagon for more information pertaining to the proof of this construction.

Proof of Construction: The proof of the inscribed regular hexagon shows that the central angles of a regular hexagon contain 60º. The central angles of the triangle inscribed in this circle contain 120º. Since ΔAOC is isosceles (OA and OC are radii lengths), m∠OCA = m∠OAC = ½ (180 - 120) = 30º. ΔAOC ΔCOB ΔBOA by SAS. By CPCTC, ∠OCB ∠OCA and m∠OCB = 30º by substitution and m∠BCA = 60º. In similar fashion, we have m∠ACB = m∠CBA = m∠BAC = 60º and equilateral ΔABC.

STEPS:
1. Place your compass point on the paper and draw a circle, O. (Keep this compass span!)

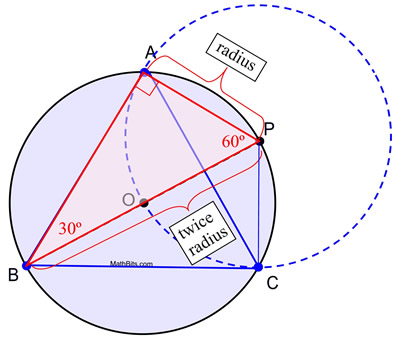
2. Using a straightedge, draw a diameter of the circle, labeling the endpoints P and B.

3. Without changing the span on the compass, place the compass point on P and draw a full circle.

4. Label the points of intersection of the two circle circumferences with A and C.

5. Draw segments from A to B, B to C and C to A, to form the equilateral triangle.

Proof of Construction: This construction uses the fact that an angle inscribed in a semicircle is a right angle, and that in a 30º-60º-90º triangle, the length of the short leg is half of the length of the hypotenuse. In this construction, circle O and circle P are congruent since they have the same radius length. AP is a radius length of circle P and radii AP = OP. OP is also a radius length of circle O (along with OB) and diameter BP = BO + OP = 2 OP. By substitution, BP = 2 AP, creating the conditions necessary for m∠ABP = 30º. Consequently, m∠APB = 60º. A similar argument can be used to establish that for ΔPBC, m∠PBC = 30º and m∠BPC = 60º making ΔPBC ΔPBA by ASA (with shared side from B to P).
Now, since they are the corresponding sides of the two congruent triangles, making ΔABC isosceles. ∠BAC ∠BCA since the base angles of an isosceles triangle are congruent.
m∠ABC = m∠ABP + m∠PBC = 30º + 30º = 60º by Angle Addition Postulate and substitution. m∠BAC + m∠BCA + m∠ABC = 180º because the sum of the angle measures in a triangle is 180º. Since m∠BAC + m∠BAC + 60º = 180º by substitution, we know 2m∠BAC = 120º and m∠BAC = 60º. Consequently m∠BCA also equals 60º by substitution, making ΔABC equilateral.