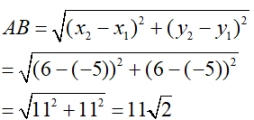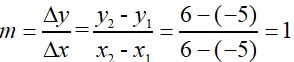|
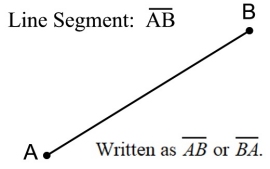
Throughout this Geometry course, we have been working with line segments, such as 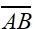 .
We have seen that this segment can be referred to as either .
We have seen that this segment can be referred to as either 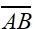 or or 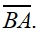 In this lesson, we are going to be examining a "directed" line segment,
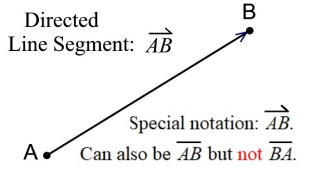
In this lesson, we are going to be examining a "directed" line segment,
where "direction" in relation to the segment will be important.
|
A directed segment is a segment that has distance (length) and direction. It is important to understand that a directed segment has a "starting point" (called the "initial point"), and an "ending point" (called the terminal point). |
|
Directed line segments are often used to represent vectors.

 |
When working in the coordinate plane, ORDER MATTERS!
Label the initial point, A, (x1, y1), and label the terminal point, B, (x2, y2). |
Order is important in controlling the "direction" on the coordinate plane,
as to whether a direction is positive (increasing) or negative (decreasing) in its movement.
|
Directed line segments and distance (length) in the Coordinate Plane:
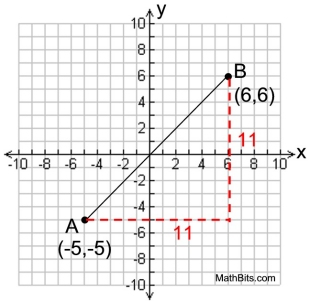  |
A directed line segment goes from
point A(-5,5) to point B(6,6).
The length of the segment (distance)
from
point A to point B
can be determined
by the Pythagorean Theorem,
(AB)2 = 112 + 112
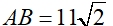
or by the Distance Formula,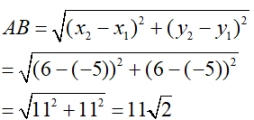 |

Directed line segments and direction (slope) in the Coordinate Plane:

 |
A directed line segment goes from
point A(-5,5) to point B(6,6).
The direction of the segment
from
point A to point B
can be represented by
the slope of the segment.
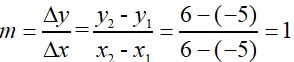
positive slope, rise 1, run 1
(from lower left to upper right)
|
Remember, when labeling the (x,y) coordintes, label the initial point as (x1,y1)
and the terminal point as (x2,y2).
If this ordering is reversed, such that Δx = x1 - x2,
the horizontal run would be -11, which is not true in this example.

See the next lessons:
Directed Line Segments: Partitions and Ratios
Partition Directed Line Segments: Methods

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|