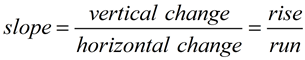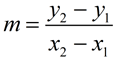GeometrySmallLogo
refresher

Let's review some information about slopes and equations of lines
that will be needed for this section on Equations.
(These skills can be reviewed further under the Linear Equations section of Algebra 1.)

Slopes
Equations of Lines
The slope of a line, m, is a rate of change which is constant in linear equations.

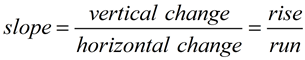
slope1

or expressed as =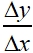
described as "delta y over delta x"
"delta", Δ, is a Greek letter meaning "change in".

When a line passes through the points
(x1, y1) and (x2, y2), the slope, m, is expressed:

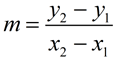
slope2

Slopes may be positive, negative, zero, or undefined(does not exist).
oscar1
Lines that have positive slope, rise from the lower left to the upper right on the axes. They go "up hill".
oscar2
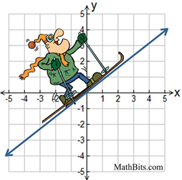
Lines that have negative slope, decline from the upper left to the lower right on the axes. They go "down hill".
oscar3
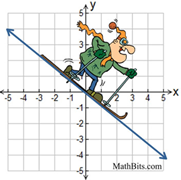
Lines that are horizontal have a slope of zero.
(There is no "rise" which creates a zero numerator.)
oscar4
Lines that are vertical have no slope (undefined slope).
(There is no "run" which creates a zero denominator.)
Depending upon the given information, equations of lines can take on several forms:

• Slope Intercept Form:
      y = mx + b
Use this form when you know, or can find, the slope, m, and the y-intercept, b.

• Point Slope Form:
      y - y1 = m(x - x1)
Use this form when you know, or can find, a point on the line (x1, y1), and the slope, m.

• Standard Form:
      Ax + By = C
The A and B values in this form cannot be zero. Use when asked to state the answer in Standard Form.
May also be Ax + By - C = 0.

• Horizontal Line Form (left/right):
      y = 7 (or any Real number)
• Lines that are horizontal have a slope of zero.
• They are parallel to the x-axis.
• They have "run", but no "rise". The rise/run formula for slope always yields zero since rise = 0.
• Every point on this line has a y-value of 7.
• When writing the equation, we have
y = mx + b
y = 0x + 7
y = 7.
• Note: The equation of the x-axis is y = 0.

• Vertical Line Form (up/down):
      x = -5 (or any Real number)
• Lines that are vertical have no slope (it does not exist, undefined).
• They are parallel to the y-axis.
• They have "rise", but no "run". The rise/run formula for slope always has a zero denominator and is undefined.
• Every point on this line has an x-value of -5.
• Note: The equation of the y-axis is x = 0.
Note:
• Lines that are parallel have equal slopes.

• Lines that are perpendicular have negative reciprocal slopes.
(A line with m = 4 will be perpendicular to a line with m = -¼)

 

Examples for Equations of Lines
Here are a few of the more common types of problems involving the equations of lines.
1. Find the slope and y-intercept of the equation 2y = 8x - 11.
Solution: First, solve for "y =".
y = 4x - 5.5
y = mx + b
The slope, m, is 4.
The y-intercept, b, is -5.5.
2. Find the equation of a line whose slope is -2 and who crosses the y-axis at (0,-3).
Solution: The m = -2 and b = -3.
y = mx + b
y = -2x + (-3)
y = -2x - 3
3. Find the equation of a line whose slope is 4 and passes through the point (-3,5).
Solution: The m = 4 and (x1, y1) = (-3,5).
Point-Slope Form
y - y1 = m(x - x1)
y - 5 = 4(x - (-3))
y - 5 = 4(x + 3)
y - 5 = 4x + 12
y = 4x + 17
4. Find the equation of a line passing through the points (-2,6) and (-4,-2).
Solution: Find slope first.
m = (6 - (-2))/(-2 - (-4)) = 8/2 = 4
Use either point as (x1, y1): (-2,6).
Point-Slope Form
y - y1 = m(x - x1)
y - 6 = 4(x - (-2))
y - 6 = 4(x + 2)
y - 6 = 4x + 8
y = 4x + 14
5. Find the equation of a line that is parallel to the line y = -2x + 8 and passes through the point (3,6).
Solution: Parallel means equal slopes.
So, m = -2 and (x1, y1) = (3,6).
Point-Slope Form
y - y1 = m(x - x1)
y - 6 = -2(x - 3)
y - 6 = -2x + 6)
y = -2x + 12
6. Find the equation of a line that is perpendicular to the line y = x + 7 and has the same y-intercept as 3y = 2x - 9. State the answer in Standard Form.
Solution: Perpendicular means negative reciprocal slopes.
So, m = -1 and b = -3.
y = mx + b
y = -1x + (-3)
y = -x - 3
x + y = -3 (Standard Form)

 


divider

NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation and is not considered "fair use" for educators. Please read the "Terms of Use".