In our study of Euclidean geometry, we have worked with two-dimensional geometry, referred to as plane geometry, and with three-dimensional geometry, referred to as solid geometry.
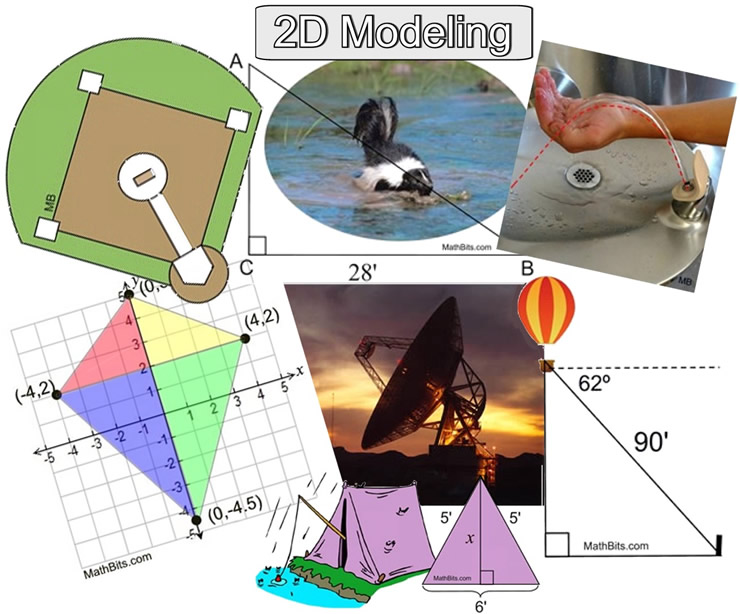
In two-dimensional geometry we modeled trajectory in water fountains with a parabola, modeled a baseball diamond with a square, modeled distance traveled by a skunk with a triangle, modeled the opening dimensions of a tent with a triangle, modeled the height of a hot air balloon with a triangle, modeled measurements of a kite on a coordinate grid, and modeled a cross section of a NASA antenna with a parabola, to mention only a few.
Now that we are working in three dimensions, we have even more options for modeling. Three dimensional geometric figures easily lend themselves to modeling objects we encounter in our everyday lives. Rectangular solids, spheres, cylinders, cones, prisms and pyramids are all around us. We live in "boxes". We play with "balls". We eat potato chips from "canisters". We lick ice cream from "cones". We reflect light through "prisms". We build "pyramidal" wonders.
Even the cells in our bodies take on geometric configurations.

The challenge of using geometric shapes as models is to find a suitable shape that best represents the object to be modeled. Common sense comes into play here. Try to use a geometric shape that most closely resembles the object, or that encloses the object with the least amount of "left over" or "empty" interior space. In certain situations, more than one shape may be needed to accomplish the task.
At a more advanced level, three dimensional software and printers are used to produce 3D models. Medical fields produce detailed models of human organs using MRI and CT scans. Science produces models of chemical compounds and even geological models for study. Architects and engineers produce scale models of buildings, vehicles, and new inventions or devices.

|