|
** This page contains Postulates and Theorems about lines and parallel lines
that are not associated with "angles".
For a connection to perpendicular lines,
see
"Perpendicular Lines".
Consider these options pertaining to "lines":
• When two lines in the same plane have one common point, they are intersecting lines.
•
When two lines in the same plane have more than one point in common, the lines coincide.
These lines lie on top of one another, and actually have an infinite number of points in common.
•
When two lines in the same plane have no points in common, they are parallel lines.
• In three-dimensional space, skew lines are lines that do not intersect and are not parallel.
Postulates About Lines:
Postulate: Through any two distinct points, only one straight line can be drawn.
Postulate: If two coplanar lines intersect, then they intersect in exactly one point.
Postulate: A line contains at least two points.
Postulate: Any straight line segment can be extended indefinitely in a straight line.
|
Postulate and Theorem About Parallel Lines:
1. Postulate: In a plane, at most one line can be drawn though a point not on a given line parallel to the given line. (Parallel Postulate)
|
2.  In a plane, if two lines are parallel to a third line, they are parallel to each other.
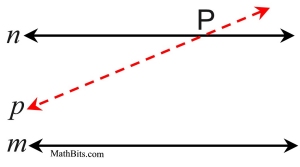
If n | | m and p | | m, then n | | p.
Indirect Proof:
• There are only two possibilities: n | | p or
n is not | | to p.
In a plane, two straight lines are parallel or they intersect.
• Assume n is not || p. Since the lines are not parallel, they must intersect at one point, call it P. Two straight lines can intersect in only one point. This is an assumption leading to a contradiction.
• Since it is given that n | |
m and p | | m, we now have two lines through P that are parallel to m. BUT, in a plane, through a point not on a line, there is one, and only one, parallel to the line (Parallel Postulate).
• The assumption leads to a contradiction.
• Therefore: n | | p
|
Indirect Proof
|
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|
