Given Too Much Information
Be aware that a question may purposely give "extra" information as a distractor.
In this problem, 32 and 28 are NOT needed to compute the area.
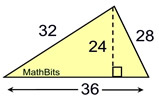 |
Find the area.
Area = ½ (24)(36)
= 432 sq.units |
|
Pairing the Correct Information
In area problems involving "base" and "height", be sure to use the height and base that are perpendicular. The 18 should not be used, in this question, to compute area.
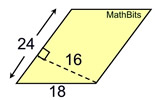 |
Find the area of this parallelogram
Area = (16)(24)
=384 sq. units
|
|
Looking Carefully at Diagram
When working with obtuse triangles, it may be necessary to look outside the triangle to find the height.
In this problem, the height paired with 18 is 16, not 12.
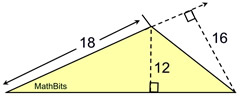 |
Find area.
Area = ½(18)(16)
= 144 sq.units
|
|
Two-step Problems
It may be necessary in certain problems to find an additional piece of information before you can find the area. This problem needs Pythagorean Theorem to find missing height.
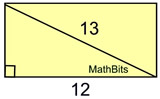 |
Find area of rectangle.
132 = h2 + 122; h = 5
A = (12)(5) = 60 sq.un.
|
|
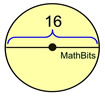
Choose the Correct Information
When working with circles, be careful to choose correctly between radius and diameter.
When finding area, you need the radius. In this problem, use radius of 8, not the d = 16.
 |
Find the area.
Round to nearest tenth.
Area = π•r2 = π•82 = 64π
= 201.1 sq.units
|
|
Be Open to New Diagrams
When working with a trapezoid, the height may be measured anywhere between the two bases. It may not necessarily form a triangle.
Look carefully at diagrams.
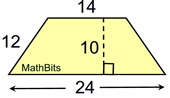 |
Find area.
A=½h(b1+b2)
=½(10)(14+24)
=190 sq. units
|
|
