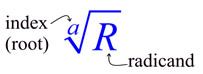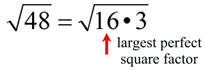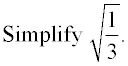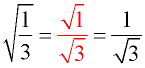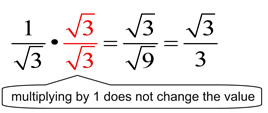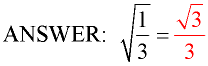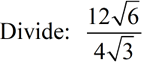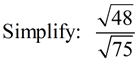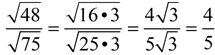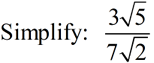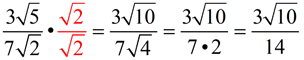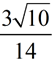Simplifying & Arithmetic Numerical Work with Square Roots MathBitsNotebook.com Topical Outline | Geometry Outline | MathBits' Teacher Resources Terms of Use   Contact Person: Donna Roberts

Remember: To "simplify a radical" does not mean to estimate the radical in decimal form.
To "simplify a radical" means to express the radical in another "form"
which is equivalent to the given radical.
This new "form" will most likely contain another radical.

A square root is in simplest form when 1. the radicand contains no perfect square factors 2. the radicand is not a fraction 3. there are no radicals in the denominator of a fraction.

• Find the largest perfect square factor (the largest perfect square that divides into 48 with no remainder). You need to be familiar with a list of perfect squares.

                   
• Give each factor its own radical sign.

• Reduce the "perfect square" radical that was created.
                   

• ANSWER:

The number out front is being multiplied times the radical, and will carry through the problem.

Separate the problem by giving the numerator and denominator their own radical symbols.
                   
While this solution may be better, it is still not in simplest form, since it leaves a radical in the denominator. You need to "rationalize the denominator".

Create a perfect square in the bottom radical by multiplying by a fraction whose value is "one".
                   

                   

Some radicals cannot be simplified. The number 23 cannot be factored by any of the perfect squares (23 is prime). This is a trick question as it is already in simplest form and cannot be reduced further.

You can add square roots when they have the same index and same radicand (number under the radical). Just add the numbers in front of the radicals.

ANS:

ANS:

To multiply square roots, multiply under the radicals and multiply any value in front of the radicals. Simplify answer if possible.

ANS:

ANS:

ANS:

To divide square roots, divide the values outside the radicals and divide the values inside the radicals.

ANS:

ANS:

To rationalize the denominator, multiply to create a perfect square under the radical in the denominator.