Practice Page
Directions: Read carefully.

1.
Two vertical angles are expressed as
(½)x + 12 and (¾)x + 8. Find the value of x.

Choose:
128
56
20
16
Angles2

 

 

2.
Two complementary angles are expressed as
4x - 16 and 2x + 10. Find the number of degrees in each angle.

Choose:
16º and 74º
42º and 48º
42º and 138º 48º and 52º
angles1

 

 

3.
∠ABD and ∠CBD form a linear pair.
If m∠ABD = 6x - 12 and m∠CBD = x + 31,
find the m∠ABD.

Choose:
27º
58º
126º 150º
Angle3

 

 

4.
AN1
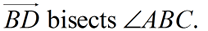
m∠ABD = 2.5x + 8.6
m∠CBD = 3.5x - 3.4
Find m∠ABC
Choose:
12º
57.9º
77.2º 38.6º
angle4

 

 

5.
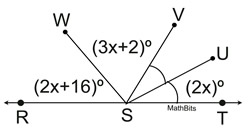
As seen in the diagram at the right:
m∠RSW = 2x + 16;  m∠WSV = 3x + 2
m∠UST = 2x;  m∠VSU = m∠UST
Find m∠WSV.
Choose:
18º
36º
52º
56º
angle5
straight <RST

 

 

6.
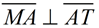anglemath2
The angles are represented as shown.
Find m∠HAT

Choose:
38º
28º
24º 22º
angle6

 

 

7.
Diagram as shown and labeled.
a) Find x.
Choose:
6½
8
15
18

b) Find m∠CMD.
Choose:
141º
115º
98º
64½º

 
angle7

 

 

8.
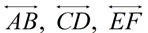
angleLines
intersecting at H.
Find x and y.
Choose:
x = 10, y = 25
x = 12, y = 23
x = 15, y = 20
x = 18, y = 17
angle8

 

 

9.
The ratio of m∠CBE to m∠DBE to m∠ABD is 1 : 2 : 3 as shown.
∠ABC is a straight angle.
Find m∠DBE.
Choose:
30º
60º
90º 120º
angle9

 

 

10.
In the diagram at the right,
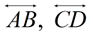
anglesmath4
and angles are labeled.
Find m∠AED.
Choose:
60º
 150º
120º 165º
angle10a



divider

NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation
 and is not considered "fair use" for educators. Please read the "Terms of Use".