definition
An exterior angle of a triangle is an angle formed by one side of the triangle and the extension of an adjacent side of the triangle.

    exdiagram1
FACTS:
• Every triangle has 6 exterior angles, two at each vertex.
• Angles 1 through 6 are exterior angles.
• Notice that the "outside" angles that are "vertical" to the angles inside the triangle are NOT called exterior angles of a triangle.


theorem1
The measure of an exterior angle of a triangle is equal to the sum of the measures of the two non-adjacent interior angles.
(Non-adjacent interior angles may also be referred to as remote interior angles.)

extdiagram

exdiagram2
FACTS:
• An exterior ∠ is equal to the addition of the two Δ angles not right next to it.
140º = 60º + 80º;        120º = 80º + 40º;
100º = 60º + 40º
• An exterior angle is supplementary to its adjacent Δ angle. 140º is supp to 40º
• The 2 exterior angles at each vertex are = in measure because they are vertical angles.
• The exterior angles (taken one at a vertex) always total 360º

Examples:

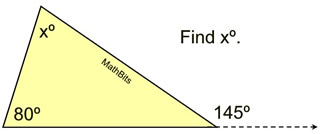1. exYellow
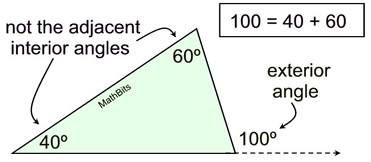
Solution: Using the Exterior Angle Theorem
145 = 80 + x
x = 65

Now, if you forget the Exterior Angle Theorem, you can still get the answer by noticing that a straight angle has been formed at the vertex of the 145º angle. See Example 2.
2. exDiagram2
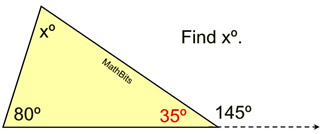Solution: I forgot the Exterior Angle Theorem.
The angle adjacent to 145º will form a straight angle along with 145º adding to 180º. That angle is 35º.
Now use rule that sum of ∠s in Δ = 180º.
35 + 80 + x = 180
115 + x = 180
x = 65
3. exWhite
Find m∠DBC.
Solution:∠BDC is an exterior angle for ΔABD.
m∠BDC = 35 + 25
m∠BDC = 60º
180 = m∠DBC + 60 + 60
m∠DBC = 60º
4. exWhite2
Find xº.
Solution:
100 = x + 50
x = 50º

dividerdash

 

Traditional Proof of the Theorem

The proof of this theorem will utilize linear pairs and the sum of the interior angles of a triangle.
exProofGiven
 extproofdiagram
Statements
Reasons
1. exproof2
1. Given
2. ∠2 and ∠4 form a linear pair
2. A linear pair is 2 adjacent ∠s whose non-common sides form opposite rays.
3. ∠2 supp ∠4
3. If 2∠s form a linear pair, they are supplementary.
4.  m∠2 + m∠4 = 180
4. Supplementary ∠s are 2 ∠s the sum of whose measures is 180.
5.  m∠1 + m∠2 + m∠3 = 180
5. The measures of the angles of a triangle add to 180º.
6.  m∠2 + m∠4 = m∠1 + m∠2 + m∠3
6. Substitution
7.  m∠2 = m∠2
7. Reflexive Property (or quantity is = itself)
8.  m∠4 = m∠1 + m∠3
8. Subtraction of Equalities



divider

NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation
 and is not considered "fair use" for educators. Please read the "Terms of Use".
A