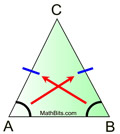
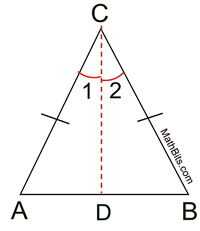
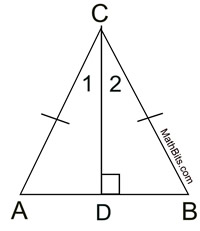
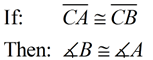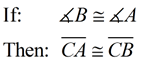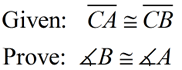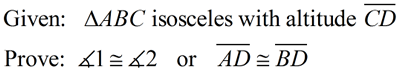definition
An isosceles triangle is a triangle with two congruent sides.
faceisosceles

An isosceles triangle is generally drawn so it is sitting on its base. This may not, however, be the case in all drawings.

These can be tricky little triangles, so beware!
isosceles triangle
hintgal
isostrio

theorem1
If two sides of a triangle are congruent, the angles opposite them are congruent. OR: The base angles of an isosceles triangle are congruent.
Converse:

If two angles of a triangle are congruent, the sides opposite them are congruent.
Theorem:
isos1isos3
Converse:
isos2isos4

Proof - Traditional



The base angles of an isosceles triangle
are congruent.
isos5
 isos3
Statements
Reasons
1. isos6
1. Given
2. Draw CD bisecting ∠ACB
2. An angle has one unique angle bisector.
3. isos7
3. An angle bisector is a ray from the vertex of the angle into the interior forming two congruent angles.
4. isos8
4. Reflexive Property (A quantity is congruent to itself.)
5. isos9
5. SAS- If 2 sides and the included ∠ of one Δ are congruent to the corresponding parts of another Δ, the Δs are congruent.
6.  isos10
6. CPCTC - Corresponding parts of congruent triangles are congruent.

 

Proof - Transformational



The base angles of an isosceles triangle
are congruent.
isos5
isos3
Proof:
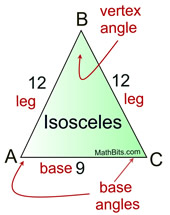
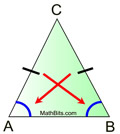
• Construct an auxiliary line through point C bisecting ∠C. An angle has a unique angle bisector. Label the intersection with the base as D.
• m∠ACD = m∠BCD because an angle bisector forms two congruent angles which have equal measure.
• Under a reflection in isos11, the reflection of C will be C, since C lies on the line of reflection.
• Since m∠ACD = m∠BCD and reflections preserve angle measure, the image of ∠ACD will be the same measure as ∠BCD.
• Since these angles are equal in measure, the reflection of ray isos12 (side of the ∠) will coincide with its image isos13 (side of the image angle).
• The reflection of isos14 will have the same length as that of isos14 since reflections preserve length.
• The reflection of isos14 will have the same length as that of isos15by substitution.
• The reflection of A is B since reflections preserve length and the segments share point C.
• The reflections of isos16 and the reflection of isos17since reflections map rays to rays.
• The reflection of ∠CAB will have the same measure as ∠CBA since reflections preserve angle measure. We have established that the rays forming these angles coincide under a reflection.
• isos18 since congruent angles are angles of equal measure.
QED

dividerdash

Altitudes in Isosceles Triangles

theorem1
The altitude to the base of an isosceles triangle bisects the vertex angle.

theorem1
The altitude to the base of an isosceles triangle bisects the base.

When the altitude to the base of an isosceles triangle is drawn, two congruent triangles are formed, proven by Hypotenuse - Leg. The altitude creates the needed right triangles, the congruent legs of the triangle become the congruent hypotenuses, and the altitude becomes the shared leg, satisfying HL. With the use of CPCTC, the theorems stated above can be proven true.

isos19

 isos4tri

 

Examples:

1.
isos5
isos20
Solution:
If two angles of a triangle are congruent the sides opposite them are congruent.
3x + 12 = 2x + 17
x = 5

AC = BC = 27 units
2.

isos6
isos21
Solution:
If two sides of a triangle are congruent the angles opposite them are congruent.
m∠CBD = 34º
m∠ACB = 68º because it is an exterior angle for ΔBCD and is the sum of the 2 non-adjacent interior angles.
m∠A = 68º from isosceles ΔABC

m∠ABC = 44º (from 180º in a triangle)
3.
isos6
isos22
Solution:
m∠2 = 38º by vertical angles.
If two sides of a triangle are congruent the angles opposite them are congruent.
m∠1 = m∠B = 71º
m∠3 = m∠D = 71º


divider

NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation
 and is not considered "fair use" for educators. Please read the "Terms of Use".