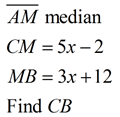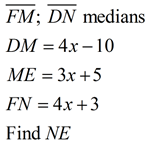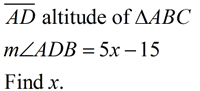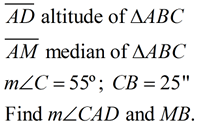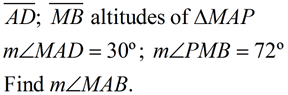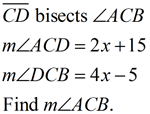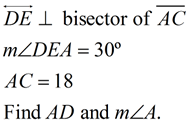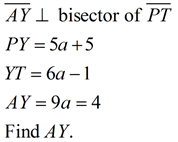|
Segments play an important role in relation to other geometric figures.
This page will examine how segments are put to use when working with triangles.
|
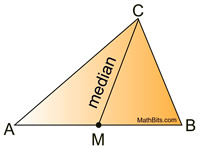
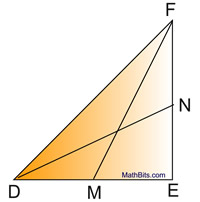
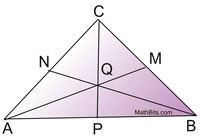
A median of a triangle is a segment joining any vertex of the triangle to the midpoint of the opposite side. |
|
|
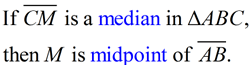
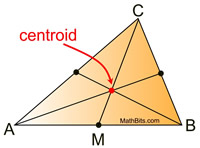
All triangles have three medians, which, when drawn, will intersect at one point in the interior of the triangle called the centroid.
|
|
The centroid of a triangle divides the medians into a 2:1 ratio. The section of the median nearest the vertex is twice as long as the section near the midpoint of the triangle's side. In other words, the length of the median from the vertex to the centroid is 2/3 of its total length.
 |
FYI: When three or more lines intersect in a single (common) point, the lines are referred to as being concurrent. The medians of a triangle are concurrent. Find out more about concurrency in the section on Constructions and Concurrency.
|
|
The median to the hypotenuse in a right triangle is equal to half of the hypotenuse. To be discussed in
the section on Right Triangles. |
|

|
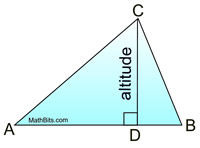
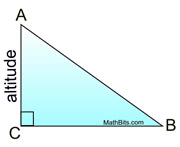
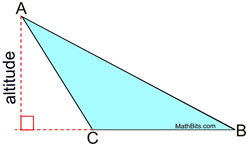
An altitude of a triangle is a segment from any vertex perpendicular to the line containing the opposite side. |
|
|
|
|
All triangles have three altitudes, which, when drawn, may lie inside the triangle, on the triangle or outside of the triangle. |
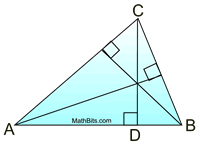
The three altitudes in an acute triangle all lie in the interior of the triangle and intersect inside the triangle. |
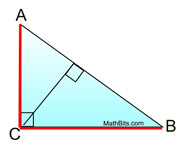
Two of the three altitudes in a right triangle are the legs of the triangle. The 3 altitudes intersect on the triangle. |
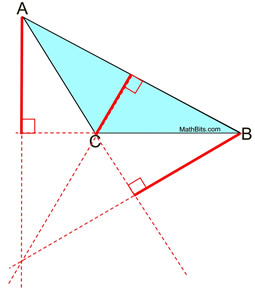 Two of the three altitudes in an obtuse triangle lie outside of the triangle. The lines containing the 3 altitudes intersect outside the triangle. Two of the three altitudes in an obtuse triangle lie outside of the triangle. The lines containing the 3 altitudes intersect outside the triangle.
|
 |
Altitudes are perpendicular and form right angles. They may, or may NOT, bisect the side to which they are drawn.
|
|
Like the medians, the altitudes are also concurrent. When drawn, the lines containing the three altitudes will intersect in one common point, either inside, on, or outside the triangle. The point where the lines containing the altitudes are concurrent is called the orthocenter of the triangle. |
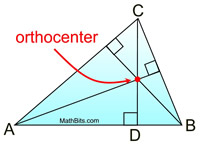
(The prefix "ortho" means "right".) |
| 1. |
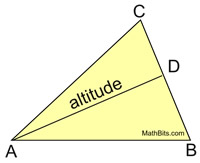 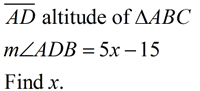 |
Solution:
altitude is perpendicular
∠ADB is a right angle of 90º.
5x - 15 = 90
5x = 105
x = 21 |
|
| 2. |
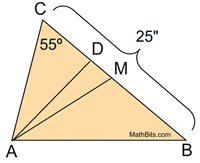 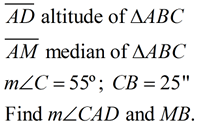 |
Solution:
The altitude will give
m∠ADC = 90º, giving
m∠CAD = 35º.
M is a midpoint so MB = 12.5 |
|
| 3. |
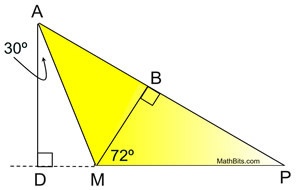 
|
Solution:
The altitudes will give right ∠ADM,
∠MBA and ∠MBP.
m∠DMA = 60º
m∠AMP = 120º (linear pair)
m∠AMB = 48º (120º- 72º)
m∠MAB =
42º (180º - (90º + 48º))
|
|

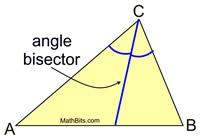
Angle Bisectors in a Triangle |
|
An angle bisector is a ray (or segment in reference to a triangle) from the vertex of the angle into the interior of the angle forming two congruent angles. |
|
|
All triangles have three angle bisectors. The angle bisectors are concurrent in the interior of the triangle. |
|
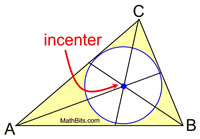
The point of concurrency is called the incenter, and is the center of an inscribed circle within the triangle. This fact is important when doing the construction of an inscribed circle in a triangle.
|
An angle bisector is equidistant from the sides of the angle when measured along a segment perpendicular to the sides of the angle.
To be discussed in
the section on Constructions and Concurrency. |
|
|
The bisector of an angle of a triangle divides the opposite side into segments that are proportional to the adjacent sides.
To be discussed in the section on Similarity. |
|
| 1. |
|
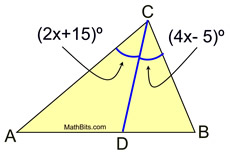
Solution:
m∠ACD = m∠DCB
2x + 15 = 4x - 5
20 = 2x
x = 10
m∠ACD = m∠DCB = 35
m∠ACB = 70º |
|
| 2. |
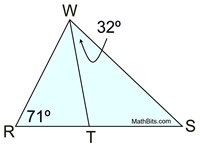  |
Solution:
m∠RWT = m∠TWS
m∠RWT = 32º
m∠RTW = 77º (180º in Δ)
m∠WTS = 103º (linear pair)
(This could also be done using ∠WTS as an exterior angle for ΔRWT.) |
|
| 3. |
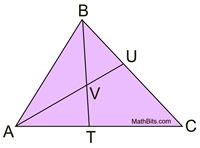 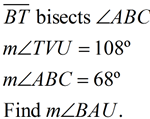 |
Solution:
m∠ABT = m∠TBC
m∠ABT = 34º
m∠AVB = 108º (vertical ∠s)
m∠BAU = 38º (180º in Δ) |
|

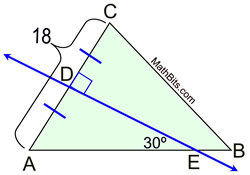
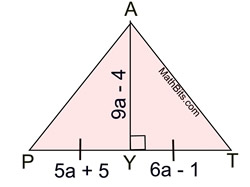
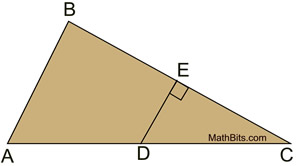
Perpendicular Bisectors in a Triangle |
|
A perpendicular bisector is a line (or segment or ray) that is perpendicular to a side of the triangle and also bisects that side of the triangle by intersecting the side at its midpoint.
The perpendicular bisector may, or may NOT, pass through the vertex of the triangle. |
|
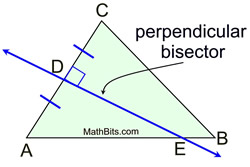 |
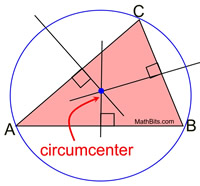
All triangles have perpendicular bisectors of their three sides. The perpendicular bisectors are concurrent, either inside, on, or outside the triangle. |
|
The point of concurrency is called the circumcenter, and is the center of a circumscribed circle about the triangle. This fact is important when doing the construction of a circumscribed circle about a triangle.



NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|