|
Once we know that two figures are similar, we also know additional information
about certain measurements involving these figures.
If we categorize length, area, and volume, it is easy to remember what happens to these measurements under similarity.
Ratio of Lengths: Perimeters, Altitudes, Medians, Diagonals, Angle Bisectors |
If two polygons are similar, their corresponding sides, altitudes, medians, diagonals, angle bisectors and perimeters are all in the same ratio.
(Note that these are all "length" measurements.)
In similar figures, if the ratio of any of these corresponding lengths is expressed as  ,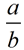
then the ratio of the other corresponding lengths can also be expressed as .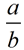
|
Example: If the corresponding sides of two similar triangles are in the ratio 2:5, what is the ratio of their perimeters?
Answer: 2:5 |
|
 NGMS Quote (pg.132): "When students use area as a device to establish results about proportions, such as the important theorem (Side-Splitter Theorem), they are making use of structure.
Ratio of Areas (square units) |
If two polygons are similar, the ratio of their areas is equal to the square of the ratio of their corresponding sides.
(Note that area is not a "length" measurement - it is a surface "area", 2-D, measurement.)
In similar figures, if the ratio of two corresponding sides (or other lengths) is expressed as ,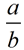
then the ratio of the areas can be expressed as .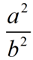
|
Example: If the corresponding sides of two similar triangles are in the ratio 3:7, what is the ratio of their areas?
Answer: 9:49 |
|
Ratio of Volumes (cube units) |
If two solids are similar, the ratio of their volumes is equal to the cube of the ratio of their corresponding sides.
(Note that volume is not a "length" measurement - it is a 3-D measurement.)
In similar figures, if the ratio of two corresponding sides (or other lengths) is expressed as ,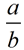
then the ratio of the volumes can be expressed as .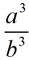
|
Example: If the sides of two cubes are in the ratio 2:3, what is the ratio of their volumes?
Answer: 8:27 |
|
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
