The page will focus on numeric and algebraic problems associated with
each of the three methods of proving triangles similar.


AA Examples:

1. Are these triangles similar?
If yes, what Similarity Theorem was used to verify the triangles similar?
If no, why not?

Solution: Yes, the triangles are similar. Each triangle has the same three angle measures,
80º, 66º and 34º.

The AA Similarity Theorem can be used to verify these similar triangles.

When given triangles with angle measures listed, be sure to check the "missing" angles before making a decision if the triangles are similar.
dividerdash

2. a. By what Similarity Theorem is ΔBDE similar to ΔBAC?

b. Find DE.

c. If EC = 20, find BE.

 Solution: a. The indication of parallel lines tells us that we have corresponding angles, ∠BDE and ∠BAC, being congruent. The AA Similarity Theorem will verify that these triangles are similar.

b. Be careful to use the FULL SIDES to find this answer.
      

c. Use either full sides or side-splitter theorem.

 

 

SSS Examples:

1. a. Are these triangles similar? Explain.

b. What is the ratio of similitude?

Solution: a. The only given information about these triangles are the side lengths. If these side lengths are proportional, the triangles will be similar by the SSS Similarity Theorem.

Does ?     Yes.
All three fractions reduce to .
Be sure to check ALL three ratios.

The triangles are similar because the corresponding sides are in proportion satisfying the SSS Similarity Theorem.

b. Ratio of similitude = .

dividerdash

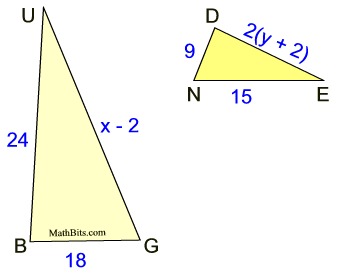
2. ΔBUG is similar to ΔDEN.
a. State the scale factor relating to these two triangles.

b. What Similarity Theorem can be used to verify that these triangles are similar?

c. Find the values of x and y.

d. Find UG and DE.

While these triangles may "look" to be right triangles, you cannot make that assumption at the beginning of this problem. As such, you cannot use the Pythagorean Theorem to find the missing sides in the triangles.
AFTER we have solved the problem, we can then verify that the triangles are right triangles.

Solution: a. Only the shortest sides of the the two triangles have numbers on them. Since the triangles are given to be similar, the scale factor between the triangles (larger to smaller) is 18 to 9 or 2 to 1.

b. SSS. Since only the side lengths are given in this problem, the triangles must be similar because the corresponding sides are in proportion satisfying the SSS Similarity Theorem.

c. The proportions: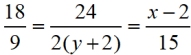     

Solve for x and y separately:

   d. UG = x - 2 = 32 - 2 = 30

   DE = 2(y + 2) = 2(4 + 2) = 2(6) = 12

 


SAS Examples:

1. a. What Similarity Theorem
can be used to show ΔBDE
to be similar to ΔBAC?

b. If given that DE = 18, find AC.

 Solution: a. The triangles share ∠B which is included between the sides of the triangles whose lengths are listed. (Use Full Sides).
Check to see that the sides are proportional.

The triangles are similar by the SAS Similarity Theorem since the congruent angle is included between the proportional sides..

b. Use the full sides since DE and AC are lengths of the full sides.

dividerdash

2. a. The triangles shown below are similar. What Similarity Theorem can be used to verify this similarity? Explain.

b. Find the value of x.

c. What is the ratio of similitude?

d. If DF = 2x + 4, find DF.

e. Find AC.

Solution: a. SAS. There is a congruent set of angles included between designated side lengths of the triangles which we know to be proportional..

b. Corresponding proportions:

c. DE = 36 and EF = 16
Compare 36:18 and 16 : 8.
The ratio of similitude is 2 : 1.

d. Substitute x = 18
2(18) + 4 = 40 = DF.

e. 2 : 1 = 40 : AC
AC = 20

 


divider


NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation
 and is not considered "fair use" for educators. Please read the "Terms of Use".