Dilations in Coordinate Plane MathBitsNotebook.com Topical Outline | Geometry Outline | MathBits' Teacher Resources Terms of Use   Contact Person: Donna Roberts

Dilation with Center at Origin, (0,0):

Formula: Center at Origin:

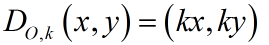
O = center of dilation at (0,0);   k = scale factor

Note that both the x and y coordinates are multiplied by the SAME value, k.

Given ΔDEF with center of dilation the origin (0,0) and scale factor of 2. D(0,4), E(1,-2), and F(-4,2) Plot ΔD'E'F'. As shown in the formula above, multiply each x and y coordinate value by the scale factor of 2 to find the new coordinates. D (0,4) becomes D' (0,8) E (1,-2) becomes E' (2,-4) F (-4,2) becomes F' (-8,4) Let the center (0,0) be labeled O: Distance from center: OF' = 2OF OE' = 2OE OD' = 2OD Length of Δ sides: F'D' = 2FD D'E' = 2DE F'E' = 2FE

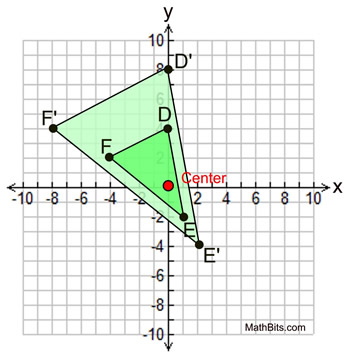
Note that the center of this dilation is "inside" the triangles.

Dilation with Center NOT at Origin:

A dilation on a coordinate axis where the center is NOT the origin can be accomplished by observing the vertical and horizontal distances of each vertex from the center of dilation. In essence, we will be looking at the "slope" of each line (segment) involved.

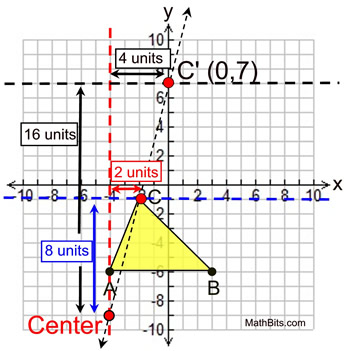
Part 1: Given point C (-2,-1) • center of dilation of (-4,-9) • scale factor of 2 • Find C'. By observation, point C is 8 vertical units above the center of dilation. Under a scale factor of 2, point C' needs to be 16 vertical units from the center. Also, point C is 2 horizontal units right of the center of dilation. Point C' needs to be 4 horizontal units right of the center. Starting at the center of dilation (-4,-9), move 4 units to the right and 16 units up to find C' at (0,7). Answer: C' (0,7) NOTE: We are maintaining the slope of the line passing through the center, point C and point C'.

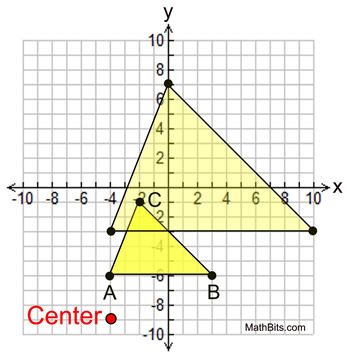
Part 2: Given points A(-4,-6), B(3,-6) • center of dilation at (-4,-9) • scale factor of 2 • Plot the dilation of ΔABC By observing vertical and horizontal distances from the center of dilation, as seen in Part 1, you can find the remaining two coordinates of the dilated triangle. Answer: A'(-4,-3), B'(10,-3), C'(0,7)

The counting of vertical and horizontal distances shown above is a simple and easy way to find the coordinates for a dilation not centered at the origin.

FYI: Another Method - Center NOT at origin
A dilation not centered at the origin, can also be thought of as a series of translations and expressed as a formula or rule. Translate the center of the dilation to the origin, apply the dilation factor as shown in the "center at origin" formula, then translate the center back (undo the translation).

• First translate the center of the dilation so the origin becomes the center.
    Subtracting the coordinate values of the center of dilation will move the center to the origin.
    Given center of dilation at (a,b), translate the center to (0,0): (x - a, y - b).

• Then apply the dilation factor, k: (k(x -a), k(y -b))

• And translate back: (k(x - a) + a, k(y - b) + b)

Formula: Center Not at Origin:

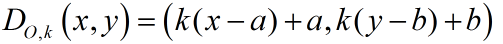
O = center of dilation at (a,b);   k = scale factor

Write a coordinate rule to find the vertices of a dilation with center (4,-2)
and scale factor of 3.

Let (x,y) be a vertex of the figure.

Translate so the origin becomes center of the dilation (left 4 and up 2): (x - 4, y + 2).

Apply the dilation formula when centered at origin: (3(x - 4), 3(y + 2)) = (3x - 12, 3y + 6)

Translate back (right 4 and down 2): (3x - 12 + 4, 3y + 6 - 2) = (3x - 8, 3y + 4)

Formula: (x,y) → (3x - 8, 3y + 4)

For example, under this dilation, the point (5,6) becomes (3(5)-8, 3(6)+4) which is (7,22).