Stretches MathBitsNotebook.com Topical Outline | Geometry Outline | MathBits' Teacher Resources Terms of Use   Contact Person: Donna Roberts

A dilation is an enlargement (or reduction) that is "uniformly" applied to a figure. The image of a dilation is the same shape as the original figure, but is not necessarily the same size. Both the vertical length and horizontal length of a dilated figure are increased (or decreased) by the same factor.

The dog on the right is a "uniform" enlargement, a dilation.

But what do we have if a transformation only changes the vertical length of a figure (or only changes the horizontal length of the figure)? What if only ONE direction is changed? If a figure is enlarged (or reduced) in only one direction, the change is referred to as a stretch. In a stretch, the figure is distorted, and is not necessarily similar to the original figure.

Horizontal Stretch ("Horizontal Dilation")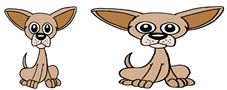 The width of the dog was increased, but the height of the dog was NOT increased. Only a horizontal change occurred.

Stretches are defined in terms of a stretch factor and an invariant line. The invariant line acts as the reference location for the stretch, somewhat like the center of a dilation. Under a stretch, the perpendicular distance from an image point to the invariant line is the stretch factor times the perpendicular distance from the pre-image point to the invariant line. You have seen stretches applied to the graphs of functions.

Vertical Stretch ("Vertical Dilation") The height of the dog was increased, but the width of the dog was NOT increased. Only a vertical change occurred.

We know that a dilation with a center at the origin and a scale factor of k
can be expressed as (x,y) → (kx, ky).
Notice that both the x and y coordinates are multiplied by the SAME value, k.

A stretch will expand the size of only ONE of the coordinates.

A stretch with stretch factor k and invariant x-axis: (x,y) → (x, ky). The x-coordinate stayed the same and the y-coordinate changed. 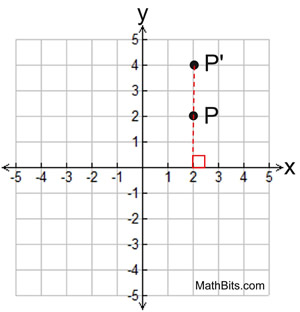P' image of P with vertical stretch factor of 2 with invariant x-axis.	A stretch with stretch factor k and invariant y-axis: (x,y) → (kx, y). The y-coordinate stayed the same and the x-coordinate changed. 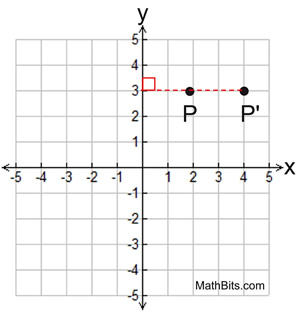P' image of P with horizontal stretch factor of 2 with invariant y-axis .
A combination of stretches: A stretch with stretch factor a in the x-direction and stretch factor of b in the y-direction: (x,y) → (ax, by). Point P was first horizontally stretched to (ax,y) and then was vertically stretched to P'(ax,by).