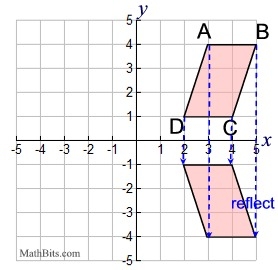
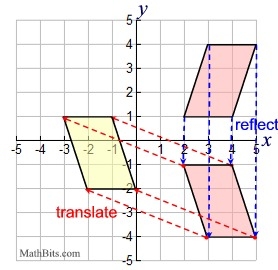
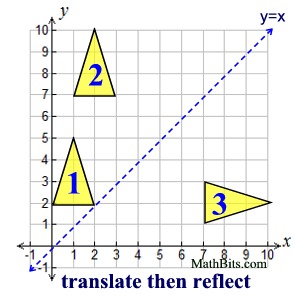
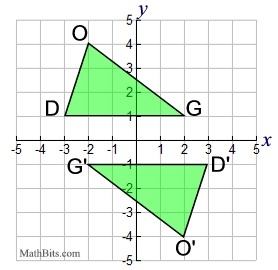
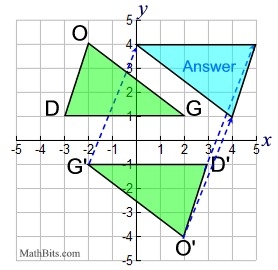
When two or more transformations are combined to form a new transformation, the result is called a sequence of transformations or a composition of transformations. In a sequence, one transformation produces an image upon which the other transformation is then applied. Example: Given quadrilateral ABCD with A(3,4), B(5,4), C(4,1) and D(2,1).
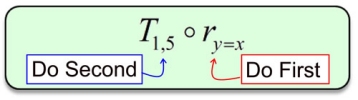
A notation such as
Now, let's take a look at these two transformations:
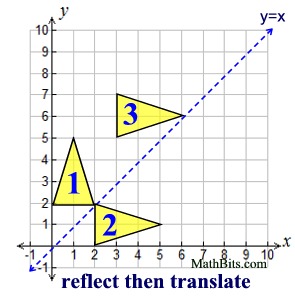
As the graphs above show, if a transformation is read from right to left,
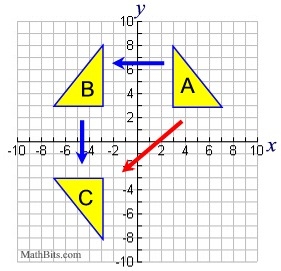
Renaming a sequence (composition): It is possible that a sequence (composition) of two transformations may be renamed by only one other transformational method. For example, the sequence (composition) of a line reflection in the y-axis followed by a line reflection in the x-axis could be described as a single transformation of a reflection in the origin (as seen in Ex. 2).
Topical Outline | Geometry Outline | MathBitsNotebook.com | MathBits' Teacher Resources
|
|||||||||||||||||||