|
We know that a sequence (or composition) of transformations
is one transformation followed by another transformation.
 |
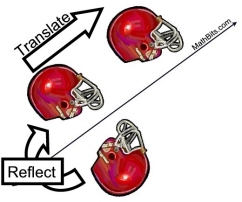When a translation (a slide or glide) and a reflection are performed one after the other, a transformation called a glide reflection is produced.
In a glide reflection, the line of reflection is parallel to the direction of the translation. It does not matter whether you glide first and then reflect, or reflect first and then glide. This transformation is commutative. |
 |
A glide reflection in the plane is the sequence (composition) of a translation and a reflection across a line of reflection, m, parallel to the directional vector line, v, of the translation. |
|
Properties preserved (invariant) under a glide reflection:
(Since these properties are preserved under both the reflection and the translation, they are preserved under the glide reflection.)
1. distance is preserved (lengths of segments are the same)
2. angle measures (remain the same)
3. parallelism (parallel lines remain parallel)
4. colinearity (points stay on the same lines)
5. midpoint (midpoints remain the same in each figure)
-----------------------------------------------------------
6. orientation NOT preserved (lettering order does not remain the same) |
|
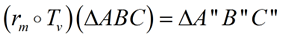
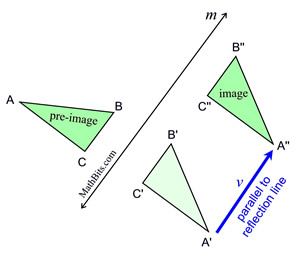 ΔA"B"C" is the image of ΔABC under a glide reflection that is a composition of a reflection over the line m and a translation through the vector v. |
In a glide reflection, the image and the pre-image will be congruent.
|
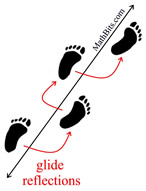
Footprints are an example of several glide reflections.
In the diagram at the left, you are seeing the original "step" on the left foot, followed by the "step" on the right foot, which is the "result" of the glide reflection.
When compared to the diagram of the triangles, shown above, you are not seeing ΔA'B'C' (reflection) in the footprints.
|
A glide reflection is an opposite rigid transformation.
A translation is a direct rigid transformation and a reflection is an opposite rigid transformation. Their sequence (or composition) is an opposite rigid transformation.
The sequence (or composition) of a direct rigid transformation and an opposite rigid transformation
is an opposite rigid transformation.
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
