|
A quick review of transformations in the coordinate plane.
("Isometry" is another term for "rigid transformation".)
Remember that a
reflection is simply a flip. Under a reflection, the figure does not change size
(it
is a rigid transformation or isometry).
It is simply flipped over the line of
reflection. The orientation (lettering of the diagram) is reversed.
Reflection
in the x-axis:
(x,y) → (x,-y)
|
When you reflect a
point across the x-axis, the x-coordinate remains the
same, but the y-coordinate is transformed into its opposite.
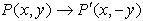 or
or 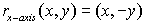
When working with the graph of y = f ( x),
replace y with - y.
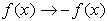 |
Reflection
in the y-axis:
(x,y) → (-x,y)
|
When you reflect a
point across the y-axis, the y-coordinate remains the
same, but the x-coordinate is transformed into its opposite.
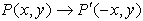 or
or 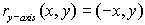
When working with the graph of y = f ( x),
replace x with - x.
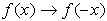 |
Reflection
in y = x:
(x,y) → (y,x)
|
When you reflect a
point across the line y = x, the x-coordinate
and the y-coordinate change places.
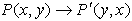
or 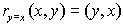 |
Reflection
in y = -x:
(x,y) → (-y,-x)
|
When you reflect a
point across the line y = - x, the x-coordinate
and the y-coordinate change places and are negated (the signs
are changed).
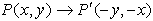
or 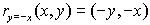 |

A
point reflection exists when a figure is
built around a single point called the center of the
figure. For every
point in the figure, there is another point found directly opposite it on
the
other side of the center. The figure does not change size (it is
a rigid transformation or isometry).
Reflection in the Origin:
(x,y) → (-x,-y)
|
While any point in the
coordinate plane may be used as a point of reflection, the most
commonly used point is the origin.
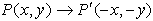 or
or 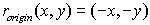
When
working with the graph of y = f ( x),
replace x with - x
and y with - y.
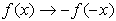 |

A rotation turns a figure through an angle about a fixed point called the center.
The center of rotation is assumed to be the origin, unless stated
otherwise. A
positive angle
of rotation turns the figure
counterclockwise, and a negative angle of rotation turns the figure
in a
clockwise direction. The figure does
not change size (it is a rigid transformation or isometry).
Counterclockwise (CCW):
referred to as positive angles
Rotation of 90º: |
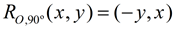 |
Rotation of 180º: |
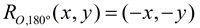 (same as reflection in origin)
(same as reflection in origin) |
Rotation of 270º: |
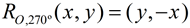 |
Clockwise (CW):
referred to as negative angles
Rotation of 90º: |
R0,90º (x,y) = (y,-x) |
Rotation of 180º: |
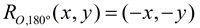 (same as reflection in origin) (same as reflection in origin) |
Rotation of 270º: |
R0,270º (x,y) = (-y,x) |
Notice how a rotation of 90º CCW is the same as a rotation of 270º CW,
a rotation of 180º CCW is the same as a rotation of 180º CW,
and, a rotation of 270º CCW is the same as a rotation of 90º CW.

A translation "slides" an object a fixed
distance in a given direction. The original object and its translation have the same shape and size (rigid transformation or isometry), and they face in the same direction. The translation may be indicated by a translation vector.
Translation of h, k:
(x,y) → (x + h, y + k)
vector: < h, k >
|
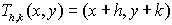 or vector < h, k > or vector < h, k >
Under 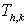 the image of y = f ( x) is y = f ( x - h) + k..
If h > 0, the original graph is shifted h units to the
right.
If h < 0, the original graph is shifted | h | units to the left.
If k > 0, the original graph is shifted k units up.
If k < 0, the original graph is shifted | k | units down. |

A dilation is not a rigid transformation.
A dilation is a
transformation that produces an image that is the same shape as the
original, but is
a different size (the figures are similar). The description of a dilation includes the scale factor
and the center of the
dilation. A dilation "shrinks" or "stretches" a figure
(and is not a rigid transformation or isometry).
Dilation of scale factor k:
(x,y) → (kx,ky)
|
The center of a
dilation is most often the origin, O. It may however, be some other point in the coordinate plane which will be specified.
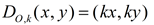 |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
