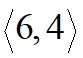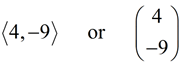|
 |
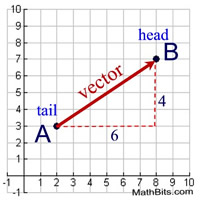
A vector is a quantity that has magnitude (length) and direction. |
|
A vector is represented by a directed line segment, a segment with an arrow at one end indicating the direction of movement. Unlike a geometric "ray", a directed line segment has a specific length.
Notation: The direction of the vector is indicated by an arrow pointing from the tail (the initial point) to the head (the terminal point). If the tail is at point A and the head is at point B, the vector from A to B can be written as:
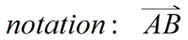
|
|
Vectors can also be represented with one bold letter, u, or one letter arrowed, 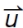 . .
(Notice the "arrow" is missing the bottom part of its feather. Be sure to use this correct arrow symbol,)
Component form is the notation we will be using on this web site.
It is also possible to designate a vector by a column notation 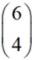 . .

Magnitude: The length (magnitude) of a vector 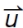 is written | is written |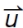 |. Length is always a non-negative real number. |. Length is always a non-negative real number.
|
The Pythagorean Theorem can be used to find the length of a vector in the coordinate plane by using the right triangle formed. The Distance Formula can also be used.
The length of the vector shown above is: 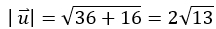

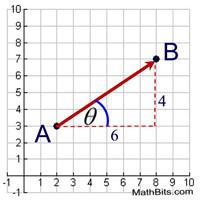
Direction: The direction of a vector is determined by the angle it makes with a horizontal line.
In the diagram at the right, the direction will be represented by theta, θ (or ∠A).
The measure of the angle can be found using a protractor, if a protractor is allowed.
Or, the value of the angle can be found using trigonometry. 
A vector is described by its magnitude and its direction.
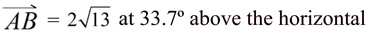
|
|

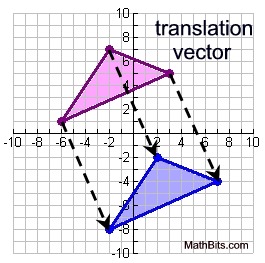
Translations and vectors:
The translation graphed at the right shows a vector translating the top triangle 4 units to the right and 9 units down. The notation for this movement can be written:
Vectors used in translations are what are known as "free vectors", which are a set of parallel directed line segments.
Any two vectors of the same length and parallel to each other are considered identical. They need not have the same initial and terminal points. The vectors in this translation, connecting the pre-image to the image, are all parallel and are all the same length.
|
|
Vectors used with translations may also be called displacement vectors or translation vectors.

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|