Practice Page
Directions: Carry the full calculator value until rounding the final answer.
1.
In ΔABC, m∠B = 82º, m∠C = 36º and a = 15 meters. Find the length b to the nearest tenth of a meter.
Choose:
19.4
17.9
16.8
15.8



LOS1

 

 

2.
In ΔRST, sin T = 2/5, sin R = 3/5, and t = 30. Find the length r.

Choose:
38
45
58
65

LOS2

 

 

3.
In isosceles ΔABC, the vertex angle is 38º and the base measures 24 inches. Find the perimeter of the triangle to the nearest inch.
Choose:
37
42
98
108
los3

 

 

4.
In ΔPQR, m∠P = 65º, p = 18 and q = 22.
Solve the triangle (find all missing sides and angles).
LOSconfused
 
Choose:
m∠Q = 22º, m∠R = 75º, r = 24
m∠Q = 23º, m∠R = 92º, r = 28
m∠Q = 32º, m∠R = 83º, r = 25
no such triangle

 

 

5.
In ΔABC, m∠A = 155º, a = 12.5 and b = 8.4. Does this data support 1 unique triangle, 2 triangles that are not congruent, or no triangles?
  Choose:
1 Δ
2 Δs
no Δs

 

 

6.
A moose is crossing a highway from marker A to marker B. A triangle connects markers A, B and C, and markers B and C are 38' apart. The angles C and B measure 70º and 60º respectively. What is the distance from point A to point B traversed by the moose (to the nearest foot)?
 
Choose:
36 feet
43 feet
47 feet
49 feet

 

 

7.
In ΔXYZ, XZ = 8, YZ = 9 and m∠X = 30º.
This triangle:
 
Choose:
must be an acute triangle.
must be a right triangle.
must be an obtuse triangle
may be either an acute triangle or an obtuse triangle.

 

 

8.
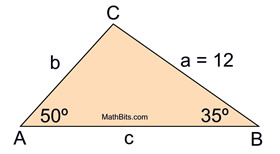
Given triangle ABC as shown at the right. Solve the triangle. (Find the remaining sides and angle.)
[If needed, round to the nearest tenth or nearest degree.]
Choose:
m∠C = 95º; b = 9.0; c = 16.0
m∠C = 95º; b = 9.2; c = 16.0
m∠C = 95º; b = 9.2; c = 15.6
m∠C = 95º; b = 9.0; c = 15.6
los8
 

 

 

9.
In ΔABC, AC = 12 and m∠A = 44º. What is the range of lengths for BC such that two distinct triangles may be created? Round to nearest tenths.

Choose:
6.4 < BC < 12
8.3 < BC < 12
8.6 < BC < 12
11.6 < BC < 12
LOS9
 

 

 

10.
Elmer creates stained glass artwork and he needs a frame for a triangular creation. He tells the frame maker that the stained glass has one angle measuring 50º with an opposite side of 10 inches, and another side of 12 inches. The frame maker correctly computes the perimeter of the stained glass artwork to be _____, to the nearest inch.
architect
 
Choose:
26"
34"
26" or 34"
34" or 36"

 

 

divider

NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation
 and is not considered "fair use" for educators. Please read the "Terms of Use".