
Simplifying a rational expression is the same process as simplifying a numerical fraction. |

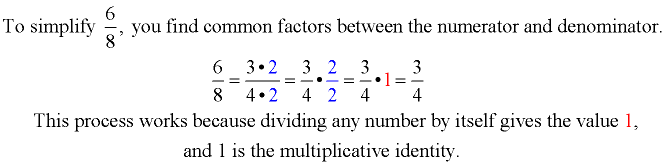 (A multiplicative identity when multiplied times a number does not change the number.)
(A multiplicative identity when multiplied times a number does not change the number.)

Steps to Simplifying Rational Expressions: |
 When determining the Domain: When determining the Domain:
Your teacher may, or may not, ask you to state the "domains" of rational expressions.
The "domains" are those values for the variable(s) that will not create zero denominators.
Simplify: 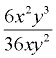 |
1. Determine the domain of the expression, looking for zero denominator problems. (may be optional)
|
1. Given: 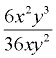 Domain: x ≠0, y≠0 Domain: x ≠0, y≠0 |
2. Factor the numerator and denominator, looking for common factors. |
2. 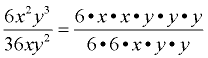 |
3. Identify the factors of 1, and write the final simplified answer (what's "left"). |
3. 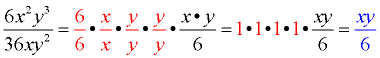 |
4. State the domain of the simplified expression. |
4. The domain of a simplified answer is always stated to be the same
as the domain of the original expression. In this case, the domain remains "all real
numbers, but not x = 0 and not y = 0". |
 In this example, the domain of the simplified expression appears to be "all real numbers",
whereas the domain of the original expression was "all real numbers but not x = 0 or y = 0." The domain of our simplified expression is NOT the same as the original domain. These two expressions are equivalent expressions, which means they have the same values (answers) for all numbers that are in BOTH domains. The numbers in both domains will be the domain of the original expression, which is the more restrictive of the two domains. In this example, the domain of the simplified expression appears to be "all real numbers",
whereas the domain of the original expression was "all real numbers but not x = 0 or y = 0." The domain of our simplified expression is NOT the same as the original domain. These two expressions are equivalent expressions, which means they have the same values (answers) for all numbers that are in BOTH domains. The numbers in both domains will be the domain of the original expression, which is the more restrictive of the two domains.
When you simplify a rational expression, keep the original domain!
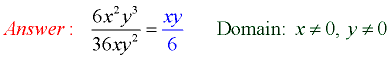
|
 When working with Monomial Terms: When working with Monomial Terms:
Simplify: 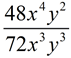 |
Things to remember:
1. There will be a larger coefficient (number out front) "left" where there was a larger coefficient to "start".
2. There will be variables
"left" where there were larger exponents to "start". (The exponent of a "left" variable is the subtraction of the exponents of those variables to "start".)
3. The domain is the domain of the original expression.
|
Example:
 |
 When working with Polynomials Terms: When working with Polynomials Terms:
Things to remember:
1. Look for factors first.
2. You cannot reduce "part" of a sum or difference.
Reduce "factors", not terms.
(In this example, the entire binomial factor was reduced.)
3. The domain is the domain of the original expression.
|
Example 1: (common factor)
 |
|