|
Check here for refreshers on Solving One-step Equations,
and Solving Two-step Equations.
Remember: Solving a linear equation is a process of undoing operations that are affecting the variable. The goal is to isolate the variable (get it alone) on one side of the equal sign.
Remember: You must always make the same changes to BOTH sides of the equal sign to "balance the equation".
Let's take a look at the types of equations that require us to deal with variables on both sides of the equal sign.
|
 |
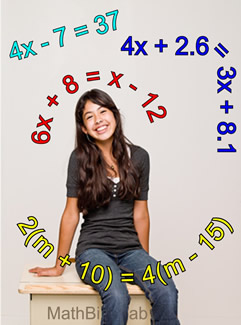 Refresh: Solving two-step equations:
|
Solve for x: 4x - 7 = 37 |
|
Analysis: More than one operation has been applied to the variable (4 has been multiplied and 7 has been subtracted). We need to undo these operations in the correct order.
First, isolate the "term" containing the x. Get 4x by itself by adding 7 to both sides.
Next, undo the multiplication by 4, by dividing both sides by 4.
This 2-step process is (1) using the additive inverse property to create a 0 on the left side (-7 + 7 = 0), and using the additive identity to isolate the 4x, since 4x - 0 = 4x.
Then (2) the process is using the multiplicative inverse to create a value of 1 and the multiplicative identity to isolate x. |
|
 |
Undo any addition or subtraction first, then undo multiplication or division.
Just remember that we never divide by zero. |
|
Check answer: A nice bonus to solving equations is that you always know if you have the correct answer. Simply substitute your answer into the original equation and see if the result is true. |
Check:
4x - 7 = 37
4(11) - 7 = 37
37 = 37 True!
|
|
When solving an equation, if your x's drop out and you end up with a statement like 12 = 12, then your equation is an identity and ALL values make it true.
If you end up with a statement like 1 = 2, then your equation is a contradiction and NO values make it true.
Read more about Truth Values of Equations.
|
|
Solving equations with variables on both sides of the equal sign:
Solve for x: 6x + 8 = x - 12 |
|
Analysis: This equation has variables on both sides of the equal sign. We need to get the x's combined into one term on one side.
"It will be easier to move" the variable with the smaller coefficient (the number multiplied times it), which in this case is the x term on the right. The sign in front of this x-term is implied to be a positive one, and one is smaller than 6, so move this term.
Subtract x from both sides.
Now, proceed as shown in the two-step example above.
|
|
|
When like-variables are scattered throughout a problem, you must get the variables together on one side of the equal sign before you can solve. |
|
Check answer: |
Check:
6x + 8 = x - 12
6(-4) + 8 = (-4) - 12
-24 + 8 = -4 - 12
-16 = -16 True!
|
|
Rather than showing all of the steps in solving an equation, some students simply think of "moving" terms across the equal sign. If you think of equations in this manner, remember that moving any term across the "equal sign" changes the term's sign. You may want to think of the = sign as a bridge. Any value crossing the bridge changes its sign.
|
|
Solving equations with multiple variables on one side of equal sign:
Solve for x: 8a + 1 - 4a + 7 = 3a + 10 |
|
Analysis: This equation has more than one term containing "a" on the left side of the equal sign. We need to get the a's combined into one term on the left side before continuing.
"Make the problem as simple as possible by combining any like terms on either side before solving."
8a + 1 - 4a + 7 = 3a + 10
8a - 4a + 1 + 7 = 3a + 10
4a + 8 = 3a + 10
Now, proceed as in the last example.
|
|
|
When combining terms, be sure to "take along" the sign in front of the term. If there is no visible sign in front of a term, it is considered to be +. |
|
Check answer:
Always check back into the original equation:
8a + 1 - 4a + 7 = 3a + 10
Do not use the combined equation:
4a + 8 = 3a + 10
You may have made an error in the creation of the "combined equation" that will not show up unless you check in the original equation.
|
Check:
8a + 1 - 4a + 7 = 3a + 10
8(2) + 1 - 4(2) + 7 = 3(2) + 10
16 + 1 - 8 + 7 = 6 + 10
16 = 16 True!
|
Solving equations containing parentheses:
Solve for m: 2(m + 10) = 4(m - 15) |
|
Analysis: This equation contains parentheses.
The first step is to get rid of the parentheses. In this problem, you need to multiply through (or across) the parentheses.
Distribute across the parentheses to get rid of the parentheses.
Now, proceed as shown in the examples above.
|
|
|
When parentheses are involved in the solution of an equation, remember the distributive property. |
|
Check answer: |
Check:
2(m + 10) = 4(m - 15)
2(40 + 10) =4(40 - 15)
2(50) = 4(25)
100 = 100 True!
|
|
If you see an equation like 5x - (3x + 2) = 14, remember that there is an implied "1" in front of the parentheses.
5x - 1(3x + 2) = 14
Distribute "-1", being careful of the signs.
5x - 3x - 2 = 14 (the solution is x = 8.)
|
|
Solving equations containing decimals (or fractions):
Solve for x: 4x + 2.6 = 3x + 8.1 |
|
Analysis: Equations may contain decimals as constants (as seen here) or as coefficients.
There is no secret to solving problems with decimals. Simply solve as you would solve an equation with integer values.
Proceed as shown in the examples above.
|
|
Check answer: |
Check:
4x + 2.6 = 3x + 8.1
4(5.5) + 2.6 =3(5.5) + 8.1
22 + 2.6 =16.5 + 8.1
24.6 = 24.6 True!
|
|
When solving equations with decimals, you can multiply all terms by a power of 10 that will remove the decimal points from the problem. Be sure you remove any parentheses from a problem before attempting this approach. Be sure to multiply carefully. The example above needs the use of 10 to the power of one.
10 • 4x +10 • 2.6 = 10 • 3x + 10 • 8.1
40x + 26 = 30x + 81 ; 10x = 55 ; x = 5.5
|
|
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|
