|
We know that the absolute value of a number is always positive (or zero).
We can see this same result reflected in the graph of the absolute value parent function y = | x |. All of the graph's y-values will be positive (or zero).
The graph of the absolute value parent function is composed of two linear "pieces" joined together at a common vertex (the origin). The graph of such absolute value functions generally takes the shape of a V, or an up-side-down V. Notice that the graph is symmetric about the y-axis.
Linear "pieces" will appear in the equation of the absolute value function in the following manner:
y = | mx + b | + c
where the vertex is (-b/m, c) and the axis of symmetry is x = -b/m. |
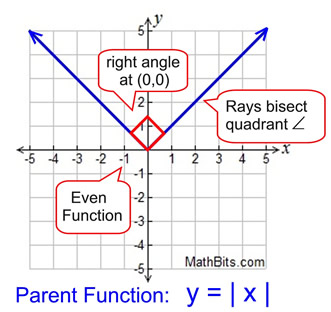 Note that the slope of the linear "pieces" are +1 on the right side and -1 on the left side. Remember that when lines are perpendicular (form a right angle) their slopes are negative reciprocals.
Note that the slope of the linear "pieces" are +1 on the right side and -1 on the left side. Remember that when lines are perpendicular (form a right angle) their slopes are negative reciprocals. |

The absolute value function is one of the most recognized piecewise defined functions.
|
Features (of parent function):
• Domain: All Reals (-∞,∞)
Unless domain is altered.
• Range: [0,∞)
• increasing (0, ∞)
• decreasing (-∞,0)
• positive (-∞, 0) U (0, -∞)
• absolute/relative min is 0
• no absolute max (graph → ∞)
• end behavior
f (x)
→ +∞, as x → +∞
f (x)
→ +∞, as x → -∞
|
|
Symmetric:
about x = 0
unless transformed
x-intercept:
intersects x-axis at
(0, 0)
unless transformed
y-intercept:
intersects y-axis at
(0, 0)
unless transformed
Vertex:
the point (0,0)
unless transformed
|
|
Range: When finding the range of an absolute value function, find the vertex (the turning point).
•
If the graph opens upwards, the range will be greater than or equal to the y-coordinates of the vertex.
• If the graph opens downward, the range will be less than or equal to the y-coordinate of the vertex.
Average rate of change:
is constant on each straight line section (ray) of the graph.
|
|
For help with absolute value graphs on your calculator,
Click Here! |
|
|
|
|
Absolute Value Function - Transformation Examples:
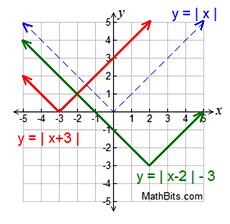 Translations
Translations |
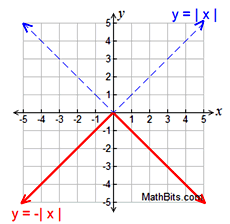 Reflection
Reflection |
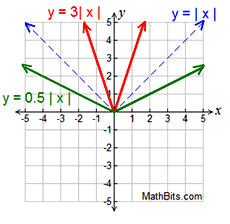 Vertical Stretch/Shrink
Vertical Stretch/Shrink
|
General Form of Absolute Value Function: f (x) = a | x - h | + k
• the vertex is at (h,k)
• the axis of symmetry is x = h
• the graph has a vertical shift of k
• the graph opens up if a > 0, down if a < 0

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|