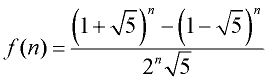Sequences as Functions - Explicit MathBitsNotebook.com Topical Outline | Algebra 2 Outline | MathBits' Teacher Resources Terms of Use   Contact Person: Donna Roberts

We saw in Sequences - Basic Information, that sequences can be expressed in various forms.
This page will look at one of those forms, the explicit form.

Sequence: {10, 15, 20, 25, 30, 35, ...}. Find an explicit formula.
This example is an arithmetic sequence(the same number, 5, is added to each term to get to the next term).

Term Number Term Subscript Notation Function Notation 1 10 a1 f (1) 2 15 a2 f (2) 3 20 a3 f (3) 4 25 a4 f (4) 5 30 a5 f (5) 6 35 a6 f (6) n an f (n) Explicit Formula: in subscript notation: an = 5n + 5 in function notation: f (n) = 5n + 5

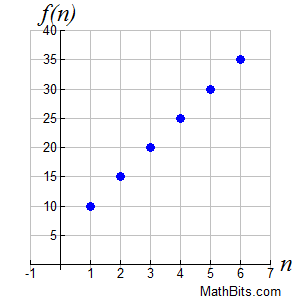
This sequence is graphed in the first quadrant. Remember that the domain consists of the natural numbers, {1, 2, 3, ...}, and the range consists of the terms of the sequence. Notice that this sequence has a linear appearance. The rate of change between each of the points is "5 over 1". While the n value increases by a constant value of one, the f (n) value increases by a constant value of 5 (for this graph). Will arithmetic sequences be linear functions?

	It is easy to see that the explicit formula works once you are given the formula. Unfortunately, it is not always easy to come up with explicit formulas, when all you have is a list of the terms. If your sequence is arithmetic, it will help if you look at the pattern of what is happening in the sequence.
Explicit formula:   f (n) = 10 + 5(n - 1) If you compare the term number with how many times the common difference, 5, is added, you will see a pattern for an explicit formula:

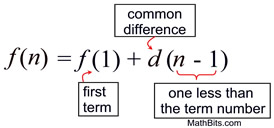To summarize the process of writing an explicit formula for an arithmetic sequence: 1. Determine if the sequence is arithmetic (Do you add, or subtract, the same amount from one term to the next?) 2. Find the common difference. (The number you add or subtract.) 3. Create an explicit formula using the pattern of the first term added to the product of the common difference and one less than the term number. 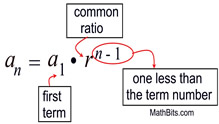an= a1 + d (n - 1) an = the nth term in the sequence a1 = the first term in the sequence n = the term number d = the common difference. {10, 15, 20, 25, 30, 35, ...} first term = 10, common difference = 5 explicit formula: an= 10 + 5(n - 1) = 10 + 5n - 5 = 5 + 5n or 5n + 5

Now that you have the explicit formula, find the 100^th term of this sequence.
Replace n with 100 in the explicit formula:   f (n) = 10 + 5(n - 1)
f (100) = 10 + 5(100 - 1) = 10 + 5(99) = 10 + 495 = 505 ANSWER

Sequence: {3, 6, 12, 24, 48, 96, ...}. Find an explicit formula.
This example is a geometric sequence (the same number, 2, is multiplied times each term to get to the next term).

Term Number Term Subscript Notation Function Notation 1 3 a1 f (1) 2 6 a2 f (2) 3 12 a3 f (3) 4 24 a4 f (4) 5 48 a5 f (5) 6 96 a6 f (6) n an f (n) Explicit Formula: in subscript notation: an = 3•(2)n-1 in function notation: f (n) = 3•(2)n-1

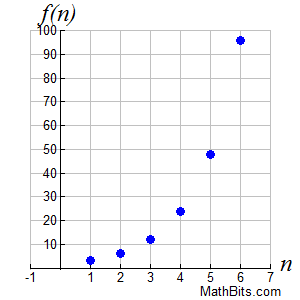
Notice that this sequence has an exponential appearance. It may be the case with geometric sequences that the graph will increase (or decrease). The rate of change will increase (or decrease) as the value of n increases (it is not constant). Will such geometric sequences be exponential functions?

	Again, it is easy to see that a given explicit formula works. The problem is coming up with a formula when all you are given is a list of the terms. If your sequence is geometric, it will help if you look at the pattern of what is happening in the sequence, in a manner similar to what we examined in the arithmetic sequence.
Explicit formula:   f (n) = 3 • 2n-1 If you compare the term number with the powers of the common difference, 2, you will see a pattern for an explicit formula:

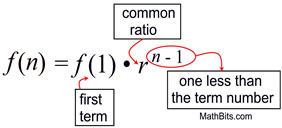To summarize the process of writing an explicit formula for a geometric sequence: 1. Determine if the sequence is geometric (Do you multiply, or divide, the same amount from one term to the next?) 2. Find the common ratio. (The number you multiply or divide.) 3. Create an explicit formula using the pattern of the first term multiplied by the common ratio raised to a power of one less than the term number. an = the nth term in the sequence a1 = the first term in the sequence n = the term number r = the common ratio {3, 6, 12, 24, 48, 96, ...} first term = 10, common ratio = 2 explicit formula: an= 3 • 2n-1

Sequence: {0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...}
This example is neither an arithmetic sequence nor a geometric sequence.

	Seeing the pattern for an explicit formula for an arithmetic sequence or a geometric sequence will be easy as compared to finding explicit formulas for sequences that do not fall into these categories. The sequence shown in this example is a famous sequence called the Fibonacci sequence. [It was introduced in 1202 by Leonardo Fibonacci. In its original form, the first term of the sequence was 1. By modern convention, the sequence now may begin with either 1 or 0.]
The Fibonacci sequence is famous as being seen in nature (leaf arrangements, bracts of pine cones, scales of pine cones, sunflowers, flower petals, Nautilus shells, grains of wheat, coniferous trees, bee hives, and even single cells). It is referred to as Nature's numbering system. The Fibonacci sequence is also associated with the golden ratio (1.61803), which can be seen in the ratio of two successive terms of the Fibonacci sequence (as the Fibonacci numbers grow).
Is there a pattern in the Fibonacci sequence? Yes. After the first two terms, each term is the sum of the previous two terms. Is there an explicit formula for the Fibonacci sequence? Yes. Explicit Formula: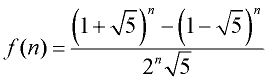 (Don't panic! You will not be asked to find explicit formulas of this difficulty level. But you may be asked to "use" a more difficult given formula.)
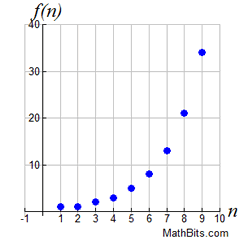
What about the graph of the Fibonacci sequence? As seen at the right, when graphed, the Fibonacci sequence takes on the appearance of an exponential graph. While it is not truly exponential, the Fibonacci sequence can be "modeled" with an exponential function. With the sequence's connection to the golden ratio, it can be "modeled" by an exponential function with 1.6 as the base, f (x) = 1.6x. (This is a "model", not an exact formula match.) See Sequences as Functions - Recursive for more information about the Fibonacci Sequence.

For calculator help with sequences click here. Arrow down to "In Func MODE"