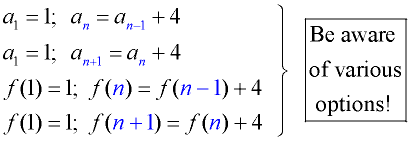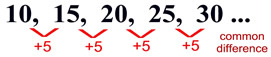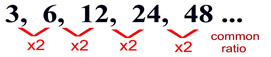|
We saw in Sequences - Basic Information, that sequences can be expressed in various forms.
This page will look at one of those forms, the recursive form.
Certain sequences (not all) can be defined (expressed) in a "recursive" form.
In a recursive formula, each term is defined as a function of its preceding term(s).
[Each term is found by doing something to the term(s) immediately in front of that term.]
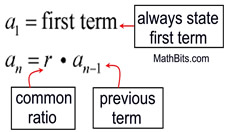
A recursive formula designates the starting term, a1, and the nth term of the sequence, an , as an expression containing the previous term (the term before it), an-1.
|
The process of recursion can be thought of as climbing a ladder.
To get to the third rung, you must step on the second rung. Each rung on the ladder depends upon stepping on the rung below it.
You start on the first rung of the ladder. a1
From the first rung, you move to the second rung. a2
a2 = a1 + "step up"
From the second rung, you move to the third rung. a3
a3 = a2 + "step up"
|
 |
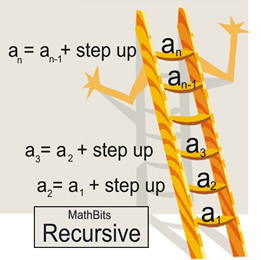If you are on the nth rung, you must have stepped on the n-1st rung. an = an-1 + "step up"
|
Notation: Recursive forms work with the term(s) immediately in front of the term being examined. The table at the right shows that there are many options as to how this relationship may be expressed in notations.
A recursive formula is written with two parts: a statement of the first term along with a statement of the formula relating successive terms.
The statements below are all naming the same sequence:
|
Given Term |
Term in front
of Given Term |
a4 |
a3 |
an |
an-1 |
an+1 |
an |
an+4 |
an+3 |
f (6) |
f (5) |
f (n) |
f (n-1) |
f (n+1) |
f (n) |
|
 Sequence:
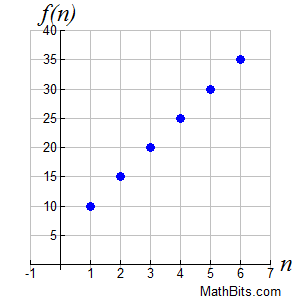
{10, 15, 20, 25, 30, 35, ...}. Find a recursive formula.
This example is an arithmetic sequence (the same number, 5, is added to each term to get to the next term).
|
Term Number |
Term |
Subscript Notation |
Function Notation |
1 |
10
|
a1 |
f (1) |
2 |
15
|
a2 |
f (2) |
3 |
20
|
a3 |
f (3) |
4 |
25
|
a4 |
f (4) |
5 |
30
|
a5 |
f (5) |
6 |
35
|
a6 |
f (6) |
n |
|
an |
f (n) |
Recursive Formulas:
in subscript notation: a1 = 10; an = an-1+ 5
in function notation: f (1) = 10; f (n)= f (n-1)+ 5 |
|
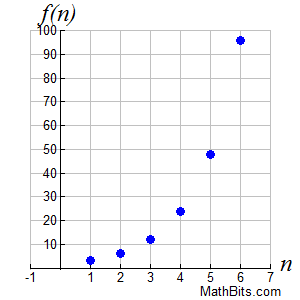
Arithmetic sequences are linear in nature. Remember that the domain consists of the natural numbers, {1, 2, 3, ...}, and the range consists of the terms of the sequence. It may be the case with arithmetic sequences that the graph will increase or decrease.
|
| |
|
In most arithmetic sequences, a recursive formula is easier to create than an explicit formula. The common difference is usually easily seen, which is then used to quickly create the recursive formula.
  |
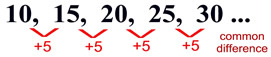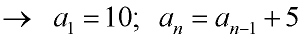To summarize the process of writing a recursive formula for an arithmetic sequence:
1. Determine if the sequence is arithmetic (Do you add, or subtract, the same amount from one term to the next?)
2. Find the common difference. (The number you add or subtract.)
3. Create a recursive formula by stating the first term, and then stating the formula to be the previous term plus the common difference.
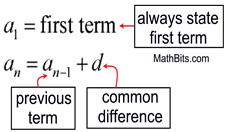
a1 = first term;
an= an-1 + d |
a1 = the first term in the sequence
an = the nth term in the sequence
an-1 = the term before the nth term
n = the term number
d = the common difference. |
|
{10, 15, 20, 25, 30, 35, ...} |
first term = 10, common difference = 5
recursive formula: a1= 10; an= an-1 + 5 |
|
 Sequence:
{3, 6, 12, 24, 48, 96, ...}. Find a recursive formula.
This example is a geometric sequence (the same number, 2, is multiplied times each term to get to the next term).
Term Number |
Term |
Subscript Notation |
Function Notation |
1 |
3 |
a1 |
f (1) |
2 |
6 |
a2 |
f (2) |
3 |
12 |
a3 |
f (3) |
4 |
24 |
a4 |
f (4) |
5 |
48 |
a5 |
f (5) |
6 |
96 |
a6 |
f (6) |
n |
|
an |
f (n) |
Recursive Formulas:
in subscript notation: a1 = 3; an = 2 • an-1
in function notation: f (1) = 3; f (n) = 2 • f (n-1)
|
|
Notice that this sequence has an exponential appearance.
It may be the case with geometric sequences that the graph will increase or decrease.
|
 |
In most geometric sequences, a recursive formula is easier to create than an explicit formula. The common ratio is usually easily seen, which is then used to quickly create the recursive formula.
  |
| |
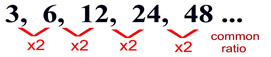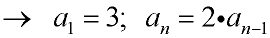To summarize the process of writing a recursive formula for a geometric sequence:
1. Determine if the sequence is geometric (Do you multiply, or divide, the same amount from one term to the next?)
2. Find the common ratio. (The number you multiply or divide.)
3. Create a recursive formula by stating the first term, and then stating the formula to be the common ratio times the previous term.
a1 = first term;
an= r • an-1 |
a1 = the first term in the sequence
an = the nth term in the sequence
an-1 = the term before the nth term
n = the term number
r = the common ratio |
|
{3, 6, 12, 24, 48, 96, ...} |
first term = 3, common ratio = 2
explicit formula: an= 3 • 2n-1
|
|
 Sequence:
{0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...}
This example is neither an arithmetic sequence nor a geometric sequence.
 |
While we have seen recursive formulas for arithmetic sequences and geometric sequences, there are also recursive forms for sequences that do not fall into either of these categories.
The sequence shown in this example is a famous sequence called the Fibonacci sequence. |
Is there a pattern for the Fibonacci sequence?
Yes. After the first two terms, each term is the sum of the previous two terms.
Is there a recursive formula for the Fibonacci sequence?
Yes. f (1) = 0; f (2) = 1; f (n)= f (n - 1) + f (n - 2)
or
a1 = 0; a2 = 1; an = an-1 + an-2
|
|
Notice that it was necessary to declare the first and second term, before stating the formula for generating the remaining terms. |
|
|
|
Arrow down to
"In Func MODE" |
|
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
