|
Sometimes there are "weird" alternative ways to work with mathematics,
and some of those ways are worthwhile and others are too confusing to be considered helpful.
Here is one alternative that you might want to consider for reflection in a line.
Read through the description to see how this method is connected to a previous construction.
 The discussion will start with a look at a different construction that we already know: The discussion will start with a look at a different construction that we already know:
construction of a perpendicular to a line through a point not on the line.

This is the construction of a perpendicular to a line from a point not on the line
(The line segments forming the triangles have been added to the diagram.) |
 |
 Note: In the construction being studied, the radius, after drawing the first arc,
was increased in length. Note: In the construction being studied, the radius, after drawing the first arc,
was increased in length.
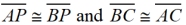
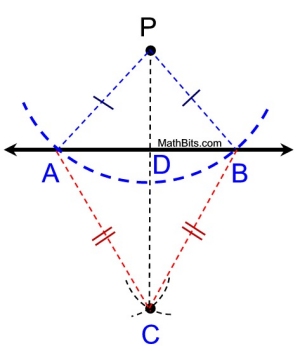
Quadrilateral APBC is a geometrical "kite".
Remember this "shape".
Kite properties include 2 pairs of adjacent sides of equal length, diagonals that are perpendicular, one diagonal forming two isosceles triangles, and one diagonal that bisects the other diagonal.
So, AD = BD, PD ≠ CD, and 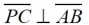
|
|
 Let's extend, and add, a couple of circles on the diagram: • The blue dashed arc (from circle P) has been extended to show the entire circle. The radius of circle P is equal in length to both AP and BP.
• In a similar manner, the red dashed arc (from circle C) has been added to the diagram. The radius of circle C is equal in length to both AC and BC.
Let's focus on point A and point B.
From the construction we know 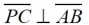
From the isosceles and congruent triangles in this diagram, we know AD = BD.
 is the perpendicular bisector of is the perpendicular bisector of 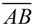 . . |
 Point A is a reflection of point B across the line of reflection Point A is a reflection of point B across the line of reflection
from P to C. (or B is the reflection of A) |
Here is the diagram without the FULL circles, but with the added red arc.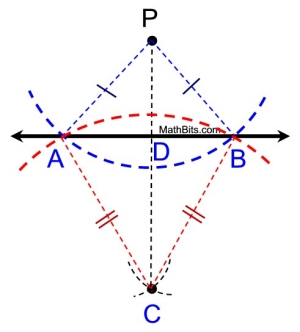 |
Perhaps it is easier to see the reflection if the diagram is rotated 90º CCW.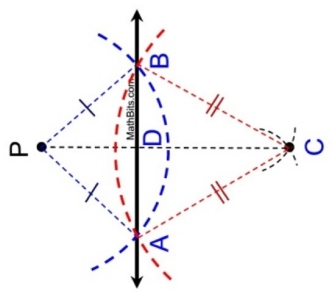 |
• Here is our new observation from this old construction of a perpendicular:
Point A is the reflection of Point B over the line through P and C.
The distance BD = DA (equidistance) with the line from P to C (as the line of reflection).
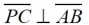 established as a perpendicular bisector. established as a perpendicular bisector.
• How can this be a new (alternative) reflection construction?
TASK: Reflect point B over a line through P and C, as shown below,
with this new alternative construction method. Label the reflection to be point A.
NEW METHOD: See the construction steps below the diagrams.
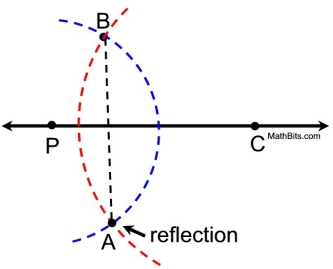
All that is needed is the construction of arcs from P and C passing through B (the point to be reflected.).
Points P and C can be anywhere on the reflection line. |
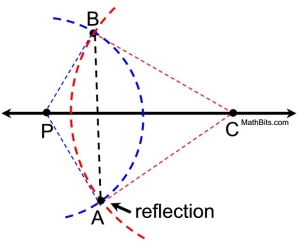
If we draw the segments connecting the points, you can see the quadrilateral kite shape which possesses all of the properties needed to prove this construction works. |
|
 This alternative method uses the following steps: This alternative method uses the following steps:
1. Designate two points "anywhere" on the line, say P and C.
2. Using those points as the centers of circles,
draw one arc
from point P through point B,
and one arc from point C
through
point B, so the arcs intersect over the reflection line.
3. Where the arcs intersect (on the opposite side of the line)
will be the reflection of point B. Label this point A.
Done.
These steps will allow for the previous diagram of a "kite" to be established,
verifying that the reflection of point B in the line of reflection will be point A.
|
Example:
Reflect ΔFUN over line m using this alternative method.
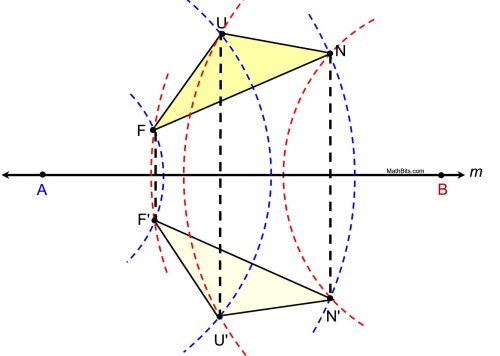
In this construction, points A and B were used for all three vertex reflections.
You could have, instead, used two points on line m for "each" of the reflection vertices.
For either method, three quadrialteral "kites" can be formed to establish the proof.
NOTE: The arcs in this construction resemble the "crayfish" looking arcs we saw in the segment bisector construction. These arcs are NOT bisecting anything!! Notice how they are not symmetric because the radii of the arcs are not the same lengths. The "crayfish" arcs were symmetric with radii of equal lengths.
 In your math class, you most likely learned the "classic" construction for reflections. If you decide to use this construction method in class, be sure to tell your teacher what you are doing. Your teacher may not be familiar with this alternative construction, and may mark your use of it as incorrect. In your math class, you most likely learned the "classic" construction for reflections. If you decide to use this construction method in class, be sure to tell your teacher what you are doing. Your teacher may not be familiar with this alternative construction, and may mark your use of it as incorrect.
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|