 |
Remember -- use your compass
and straightedge only! |
|
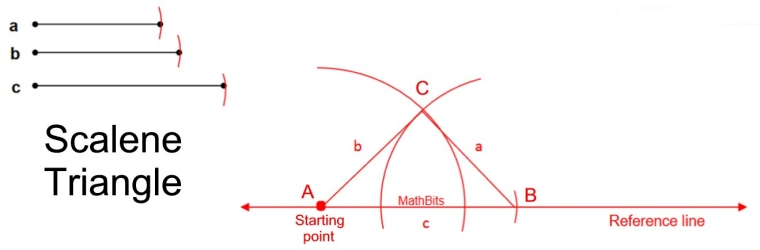
1. Scalene Triangle 2. Isosceles Triangle 3. Equilateral Triangle
|
All three styles of triangles will be addressed on this page.

1. Construct a Triangle Given 3 Sides: Scalene |
|
Given: 3 segments of varying lengths
Construct: a triangle, ΔABC, using these segments as sides
(Uses copying segments.)
|
 |
STEPS:
1. Draw a reference line as a place to start the triangle. Mark a starting point on the line.
2. Copy one of the segments onto the reference line (preferably the longest side, c).
3. Use the compass to measure the length of one of the other two sides (such as b).
4. Place the compass point on the same starting point. Without changing the size of the compass, make an arc above the reference line. Make a generous amount of the arc as you don't know where the other side might cross this arc. While it is not required, your arc can cross the reference line.
5. Copy the last segment (in this case, a).
6. Place the compass point at the other end of segment c marked on the reference line. Make an arc that will intersect with the previous arc, above the reference line.
7. Connect both end points of segment c to the intersection of the arcs above the reference line. The triangle has been formed.

Proof of Construction: The construction makes 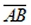 congruent to segment c, congruent to segment c, 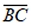 congruent to segment a, and congruent to segment a, and 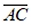 congruent b. Hence, ΔABC is the desired triangle. congruent b. Hence, ΔABC is the desired triangle.
2. Construct a Triangle Given 2 Sides: Isosceles |
|
Given: 2 segments of varying lengths (for "base", and "legs")
Construct: a triangle, using these segments as sides
(Uses copying segments.)
|
|
STEPS:
The steps are the same as those for a scalene triangle. Simply use the segment labeled legs twice
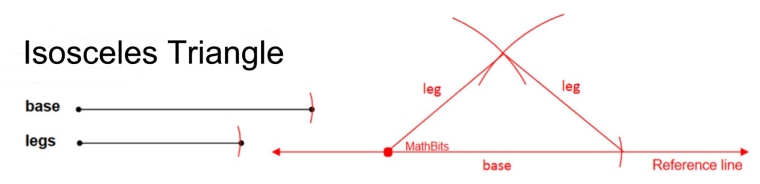
Proof of Construction: The same premise as that for the scalene triangle.
3. Construct a Triangle Given 1 Side: Equilateral |
|
Given: 1 segment (as a "side")
Construct: a triangle using this one segment
(Uses copying segments.)
|
|
STEPS:
The steps are the same as those for a scalene triangle. Simply use the one segment 3 times.
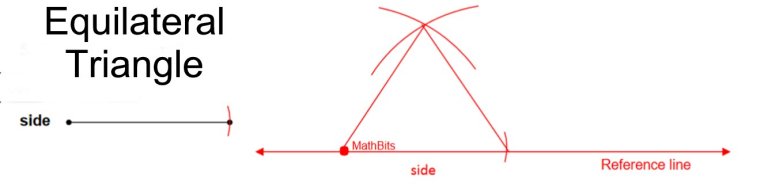
Proof of Construction: The same premise as that for the scalene triangle.
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|