Two lines are parallel if and only if they lie in the same plane and do not intersect. Parallel lines never cross.

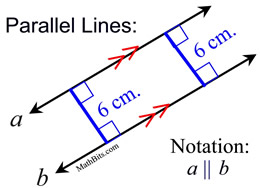
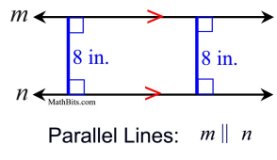
Parallel lines are always the same distance apart, which is referred to as being "equidistant".
For our purposes, parallel lines will always be straight lines that go on indefinitely.
The parallel lines may be horizontal, vertical or slanted.

Parallel lines are marked with "feathers" (arrows) such as > or >>.
The notation to indicate parallel lines are two vertical bars | |.
Line m being parallel to line n is written m | | n.

Segments and rays may also be described as being parallel
when the lines containing these segments or rays are also parallel.

A transversal is simply a line that intersects two or more lines in the same plane. The intersected lines may, or may not, be parallel.

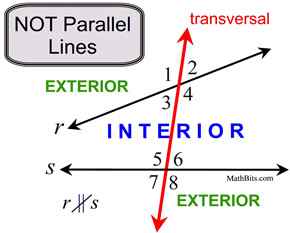
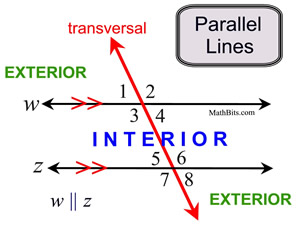
When lines intersect, a series of angles are formed. Certain angles are given specific "names" based upon their locations in relation to the lines. These specific names may be used whether the lines involved are parallel or not parallel.

Each diagram above shows eight angles formed by the transversal and the two lines with which it intersects. The term "INTERIOR" refers to the space "between" those two lines, while the term "EXTERIOR" refers to the spaces that are not between those two lines (i.e. the 2 outer regions).

Two lines are perpendicular if and only if they form a right angle.

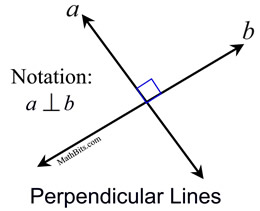
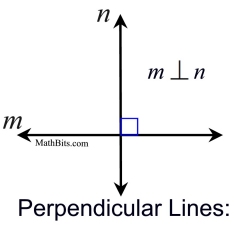
Perpendicular lines always form a right angle of 90º.
While perpendicular lines may appear in a slanted or a horizontal position on paper,
the lines must always intersect to form a right angle.

(slanted positions)

(horizontal/vertical positions)

Perpendicular lines are marked with a "square" (a box) drawn at the point of intersection.
The notation to indicate perpendicular lines is ⊥.
Line m being perpendicular n is written m ⊥ n.

Segments and rays may also be described as being perpendicular
when the lines containing these segments or rays are also perpendicular.