Also see "Perpendicular Bisectors in a Triangle" at Segments in Triangles.

def
A perpendicular bisector of a given line segment is a line (or segment or ray) which is perpendicular to the given segment and intersects the given segment at its midpoint (thus "bisecting" the segment).
perpdiagram2

perep2statement

perpd2given


Theorem
The perpendicular bisector of a line segment is the set of all points that are equidistant from its endpoints. To be discussed further in the section on Constructions.

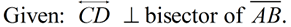
perpdiagram3given

Every point on the perpendicular bisector, cd, is the same distance from point A as it is from point B.

AC = CB
AF = FB
AG = GB
AE = EB
AH = HB
AJ = JB
AD = DB

You can think of the points on the perpendicular bisector as being the third vertices of a series of isosceles triangles with vertices A and B.
perpdiagram3

dividerdash

Theorem Proof: (transformational method)
perpbisproof1a
perpbisproof2
1. A perpendicular bisector of a segment (by definition) is a line that is perpendicular to the segment and intersects the segment at its midpoint.
2. 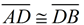perpbisproof3 because a midpoint of a segment divides the segment into two congruent segments.
3. AD = DB because congruent segments are segments of equal measure.
4. The line of reflection for a segment is the perpendicular bisector of the segment.
5. Under a reflection in perpbisproof4, A is mapped onto B, C is mapped onto C, and D is mapped onto D.
6. Under a reflection in 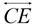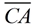perpbisproof4, perpbisproof5is mapped onto 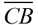perpbisproof6.

7. CA = CB since a reflection is a rigid transformation which preserves length.

dividerdash

Theorem Proof: (two-column method)
perpbisproof1a
perpbisproof2
Statements
Reasons
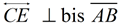1. perpbispf2
1. Given
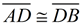2. perpbispf3
2. Segment bisector forms 2 congruent segments.
3. ∠ADC, ∠BDC are right angles
3. Perpendiculars form right angles.
4. ∠ADC 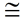congruent∠BDC
4. All right angles are congruent.
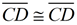5. perpbispf4
5. Reflexive property
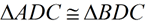6. perpbispf5
6. SAS: If 2 sides and the included angle of one triangle are congruent to the corresponding parts of another triangle, the triangles are congruent.
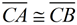7. perpbispf6
7. CPCTC: Corresponding parts of congruent triangles are congruent.
8. CA = CB
8. Congruent segments have equal measure.

 

divider


NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation
 and is not considered "fair use" for educators. Please read the "Terms of Use".