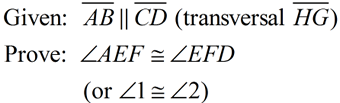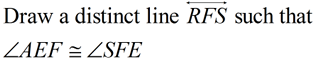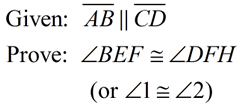|
On the page Angles and Parallel Lines, we saw four major pairs of angles associated directly
with parallel lines and the theorems stating each pairs status given the lines to be parallel.
If the lines are parallel, then ...
| 1. |
• alternate interior angles |
congruent angles
|
| 2. |
• alternate exterior angles |
congruent angles |
| 3. |
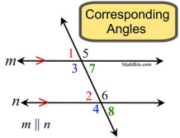
• corresponding angles |
congruent angles |
| 4. |
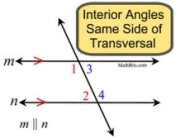
• interior angles on the same
side of the transversal |
supplementary angles |
On this page, we will prove geometrically that these associations are true.
Keep in mind that there are always several ways to prove a concept.
We will be examining one (or two) methods of proof for each angle pair.

 "Given" Parallel Lines, prove angles congruent (or supplementary) "Given" Parallel Lines, prove angles congruent (or supplementary)

In "Method 1", we will prove the following four theorems dealing with alternate interior,
alternate exterior, corresponding angles, and interior angles on the same side of the transversal.
All four angle types will be proven in one proof!!
|
If two parallel lines are cut by a transversal, the alternate interior angles are congruent. |
|
|
If two parallel lines are cut by a transversal, the alternate exterior angles are congruent. |
|
|
If two parallel lines are cut by a transversal, the corresponding angles are congruent. |
|
|
If two parallel lines are cut by a transversal, the interior angles on the same side of the transversal are supplementary. |
|
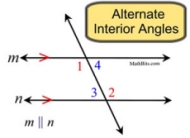
2 pair of angles |
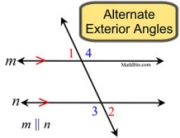
2 pair of angles |
4 pair of angles |
2 pair of angles |
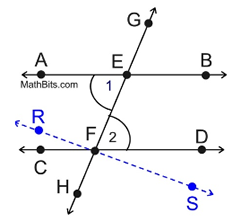
Method 1: (Two Column Proof)
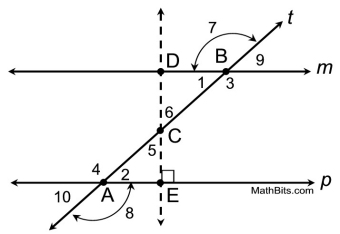
|
Given: m || p, both cut by transversal t
Prove: 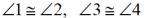 (alt.int) (alt.int)
Corollaries:
Prove: 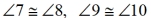 (alt.ext) (alt.ext)
Prove: 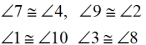 (corres) (corres)
Prove: ∠1 supp ∠4, ∠ 3 supp ∠ 2
(int. on same side of transversal) |
The idea behind this proof is to utilize congruent triangles.
An auxiliary line will be drawn to form the triangles.

Now, continue on in this proof to prove the alternate exterior angles are congruent.
Exterior angles form either a linear pair or vertical angles with the alternate interior angles
which have now been shown to be congruent.

Continue again in this proof to prove the corresponding angles are congruent.
The corresponding angles can form vertical angles with the alternate interior angles
which have been shown to be congruent.

Finish by proving the interior angles on the same side of the transversal are supplementary.
Using the previous work with linear pairs, substitution will prove these angles supplementary.

QED
 The Theorem used as "Reason #4" was proven under Perpendicular Lines using an Indirect Proof and the Parallel Postulate.
While you may see this Theorem "proven" using "corresponding angles", such a proof would not make the Theorem usable
as a reason in this proof as it would be circular reasoning. The Theorem used as "Reason #4" was proven under Perpendicular Lines using an Indirect Proof and the Parallel Postulate.
While you may see this Theorem "proven" using "corresponding angles", such a proof would not make the Theorem usable
as a reason in this proof as it would be circular reasoning.
But, since we are using a more generic alternative proof for "Reason #4", we are good to go!!


In "Method 2", we will be dealing only with a proof regarding alternate interior angles.
This proof is an indirect proof, so a different style of reasoning is being used.
|
If two parallel lines are cut by a transversal, the alternate interior angles are congruent. |
|
Method 2: (Indirect Proof)
|
1. Given |
2. 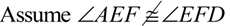 |
2. Assumption leading to a contradiction. |
3. 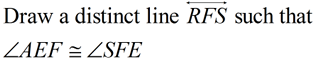 |
3. An angle may be copied. |
|
4. If 2 lines are cut by a transversal and the alternate interior angles are congruent, the lines are parallel. |
|
5. Parallel Postulate: Through a point not on a given line, only one line can be drawn parallel to the given line. |
6. 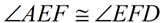 |
6. Contradiction steps 3 and 5. |
QED |


"Method 3" will demonstrate another form of proof, the transformational proof.
This proof deals with corresponding angles only.
|
If two parallel lines are cut by a transversal, the corresponding angles are congruent. |
|
Method 3: (Transformational Proof)
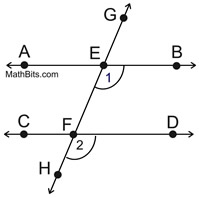
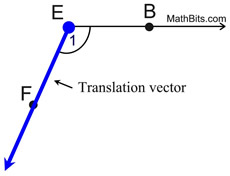
1. Let's look first at ∠BEF.
Using
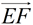 as the translation vector, slide ∠BEF down the ray such that its vertex remains on the ray and will coincide with point F. as the translation vector, slide ∠BEF down the ray such that its vertex remains on the ray and will coincide with point F.
Point F will become the image of point E. |
|
2. We now know that  When studying translations, we discovered that the corresponding sides (lines) of the pre-image and the image are parallel, since the distances between the pre-image points and image points are constant (equal).
|
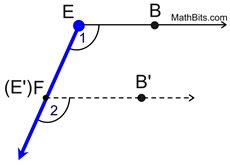 |
3. Now, is 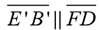 ? Yes! 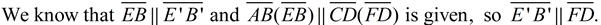
In a plane, if two lines are parallel to the same line, they will be parallel to each other.
|
4. Does 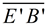 actually coincide with 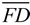 ? Yes!
Since these segments are parallel and share a common end point, F ( E'), they must be on the same line. The Parallel Postulate states that through any point ( F ) not on a given line ( 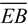 ), only one line may be drawn parallel to the given line. |
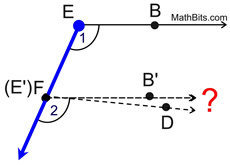 |
5. We now know that ∠1 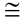 ∠2. Being a rigid transformation, translations preserve angle measure, making m∠1 = m∠2 (or congruent). |
|
QED

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|