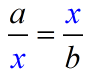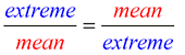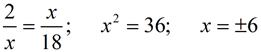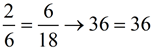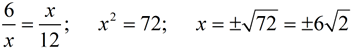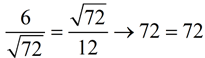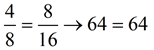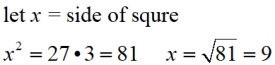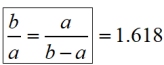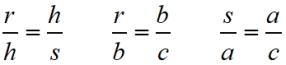|
The term "mean proportional" may also be referred to as "geometric mean".
The term "mean", when used alone, or in a context such as "mean, median, and mode",
refers to finding the "average" and is known as the Arithmetic Mean.
Mean proportional, or geometric mean, is not the same as the Arithmetic Mean. While an arithmetic mean deals with addition, a geometric mean deals with multiplication.
|
The mean proportional, or geometric mean, of two positive
|
numbers a and b is the positive number x such that 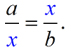 When solving, 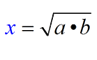 . |
Notice that the x value appears TWICE in the "means" positions of the proportion. |
|
Note*: The mean proportional (geometric mean), along with the values of a and b, are positive.
Mean
Proportional
or
Geometric Mean
|
|
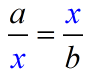
In a "mean proportional", or "geometric mean", both " means" ( x) are the exact same value. |
|
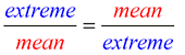 Remember the rule:
In a proportion, the product of the means equals the product of the extremes ("cross multiply").
Remember the rule:
In a proportion, the product of the means equals the product of the extremes ("cross multiply"). |
|
Examples:
1. |
Find the mean proportional between 2 and 18? |
| |
|
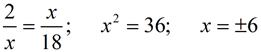 While algebraically there are two solutions for x,
While algebraically there are two solutions for x,
the mean proportional, by definition, is positive.
Answer: x = 6 |
Check answer:
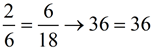
|
2. |
What is the geometric mean of 6 and 12? |
| |
|
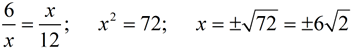 Remember, the geometric mean of two positive numbers is positive.
Remember, the geometric mean of two positive numbers is positive.
 |
Check answer: 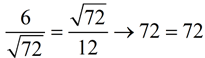 |
You can see from Example 2 that it will be necessary to remember your skills for
working with radicals. If you need a refresher, refer to Simplifying Square Roots.

3. |
The mean proportional between two values is 8. If one of the values is 16, find the other value. |
| |
|
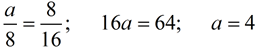 Answer: a = 4
Answer: a = 4 |
Check the answer:
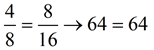 |
Notice that the "8" is placed in the "means" position in the proportion, appearing twice.

Let's check out some basic Geometry applications.
4. |
Find the side of a square whose area is the same as that of a rectangle with a length of 27 cm and a width of 3 cm. Is there a geometric mean relation? |
| |
|
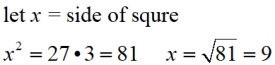 Answer: x = 9 (positive only, since
Answer: x = 9 (positive only, since
it represents length) |
9 is the geometric mean between 27 and 3.

There was a number times itself that equaled the product of two unique numbers. Such is the relationship between the area of a square equaling the area of a rectangle. |

5. |
The Greeks discovered that there is a specifically shaped rectangle that is most pleasing to the eye, called a Golden Rectangle, where the ratio of its length to its width can be estimated to be to 1.618. When this rectangle is sub-divided into a square and a rectangle, the remaining rectangle is also another Golden Rectangle. |
| |
|
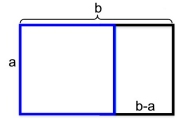
Original rectangle:
Length/width = b/a = 1.618
New, smaller rectangle:
Length/width = a/(b-a) = 1.618
|
If we compare these length/width ratios, we can see that the original width, a, is the geometric mean between the lengths of the two Golden Rectangles.
 |

 But the most important geometric connection for our purposes, But the most important geometric connection for our purposes,
is the connection with right triangles.
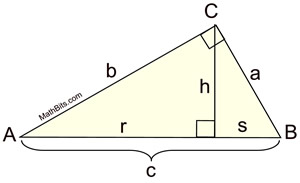
6. |
Given a right triangle, with the altitude drawn to the hypotenuse, three geometric means exist. |
| |
|
|
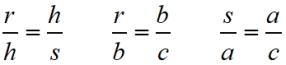
We will be working with these proportions in the upcoming lessons. |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|

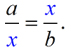 When solving,
When solving, 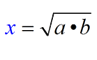 .
.