|
We have seen how inequalities can be applied to the sides and angles of a single triangle.
Now, we will take a look at how inequalities can be put to work between two triangles.
Hinge Thm |
If two sides of a triangle are congruent to two sides of another triangle and the included angle of the first is larger than the included angle of the second, then the third side of the first triangle is longer than the third side of the second triangle.
(May also be referred to as the SAS Inequality Theorem) |
|
The "included angle" is the angle formed by the two sides of the triangle mentioned in this theorem.
This theorem is called the "Hinge Theorem" because it acts on the principle of the two sides described in the triangle as being "hinged" at their common vertex.
Consider the alligator jaws at the right. |
 |
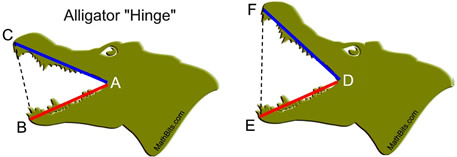The sides described in this theorem are the jaw lengths of the alligator with the "hinge" being at the corner of the alligator's mouth (point A or D). While the jaw lengths of the alligator will not change, the jaw "hinge" does allow the alligator to open, or close, its mouth with varying angular degrees (at point A or D).
|
Remember that the key fact in applying this theorem is that the two sides forming the angle will be of the same length in both triangles.
The converse of this theorem is also true.
|
If two sides of a triangle are congruent to two sides of another triangle and the third side of the first is longer than the third side of the second, then the included angle in the first triangle is greater than the included angle in the second triangle.
(May also be referred to as the SSS Inequality Theorem.) |
|
If we return to the alligator analogy, the converse of the Hinge Theorem would tell us that the wider the alligator opens his mouth (EF > BC), the larger the angle he creates at the hinge of his jaw (m∠D > m∠B). If EF > BC, then m∠D > m∠B.
|
2.
|
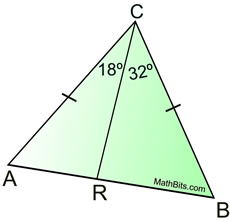
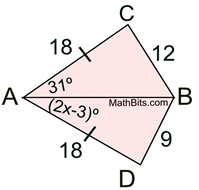Given AC = 18, AD = 18,
m∠CAB = 31º, m∠BAD = (2x - 3)º
Write an inequality, or set of inequalities, to describe the possible values for x.
|
Solution: AB = AB, so the Converse of the Hinge Theorem applies. Since CB > BD, m∠CAB > m∠BAD, and we have the inequality:
31 > 2x - 3 x < 17
34 > 2x
17 > x
Now, we should also guarantee that the angle is not negative or zero.
2x - 3 > 0
x > 3/2 or 1.5
Final Answer: 1.5 < x < 17
|
|
3.
|
|
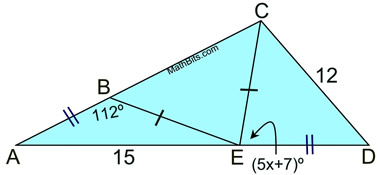
Solution:
ΔABE and ΔDEC satisfy the Converse Hinge Theorem conditions.
Since AE > CD, we know
m∠ABE > m∠CED.
112 > 5x + 7
105 > 5x
21 > x
Making sure the angle is not negative or zero we have:
5x + 7 > 0
x > -7/5 or -1.4
Final Answer:
-1.4 < x < 21 |
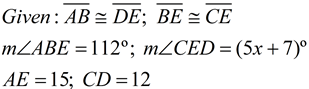
Write an inequality, or set of inequalities, to describe the possible values for x. |
|
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
, the conditions for the Hinge Theorem are satisfied, and the longer segment (side) will be opposite the larger angle.