|
Sometimes, in Geometry, a "fancy" theorem is really
just plain old common sense.
Dave is walking his dog and it starts to rain.
He wants to get from point D to point O as quickly as possible.
Should he go from point D to point G and then to point O?
Or should be go directly from point D to point O? |
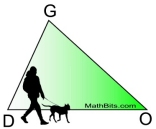 |
Of course, he should go directly from point D to point O.
The shortest distance between two points is a straight line. Meaning .DO < DG + GO. |
Keep this example in mind as you read this next Theorem.
|
The sum of the lengths of any two sides of a triangle must be greater than the third side. |
|
 |
If these inequalities are NOT true, you will not have a triangle!
|
|
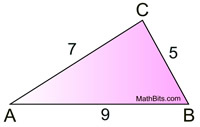
AB + AC > CB ( 9 + 7 > 5)
AC + CB > AB (7 + 5 > 9)
CB + AB > AC
(5 + 9 > 7)
|
|
This theorem may also be stated in reverse (converse) as:
The length of one side of a triangle is less than
the sum of the lengths of the other two sides.
|
In a triangle, the longest side is across from the largest angle.
In a triangle, the largest angle is across from the longest side.
|
|
Both of these theorems may also be stated using "longer" and " larger" when dealing with 2 sides and 2 angles.
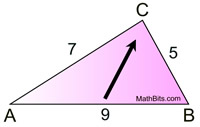
Since 9 is the longest side of the triangle,
∠ C (across from it) is the largest angle. |
|
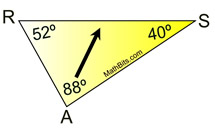
Since 88º is the largest angle of the triangle,
 (across from it) is the longest side. |
|
The measure of the exterior angle of a triangle is greater than the measure of either non-adjacent interior angle. |
|
This is one of those "common sense" theorems.
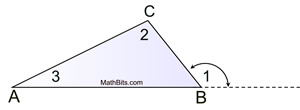
In the diagram at the right,
∠1 is an exterior angle for ΔABC.
By the Exterior Angle Theorem, m∠1 = m∠2 + m∠3.
It is common sense that m∠1 > m∠ 2 and m∠1 > m∠3.
|
|
1.
|
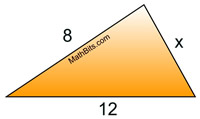 Given the 2 sides shown,
Given the 2 sides shown,
find the "possible" lengths
of the third side. |
Solution:
• 8 + x > 12, so x > 4
• x + 12 > 8, so x > -4 (no info, length positive)
• 8 + 12 > x, so 20 > x
Putting the statements together, we have x must be greater than 4, but less than 20.
4 < x < 20 |
|
2.
|
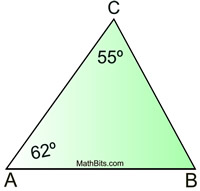 Given the 2 angles shown,
Given the 2 angles shown,
determine which side is the
"longest" side of the triangle.
|
Solution:
We must find m∠B to determine if it is larger than 62º, making it the largest angle in the triangle.
m∠A + m∠B + m∠C = 180º
62º + m∠B + 55º = 180º
m∠B = 63º, making ∠B the largest angle in the triangle.
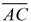 is the longest side. is the longest side.
(the side across from the largest angle)
|
|
3.
|
|
Solution:
1) Exterior Angle Theorem - TRUE
2) Inequality Theorem about Exterior Angles (stated above) - TRUE
3) Linear Pairs are supplementary (2 ∠s adding to 180) - TRUE
4) FALSE (it should read m∠1 > m∠C) |
| |
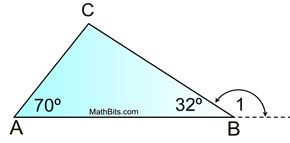
Given ΔABC as shown.
Which statement is NOT true?
1) m∠1 = m∠A + m∠C
2) m∠1 > m∠A
3) m∠1 + m∠ABC = 180º
4) m∠1 < m∠C |
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|