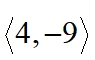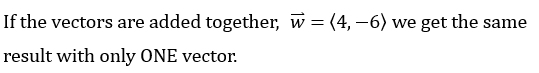|
Vectors are a convenient way to describe and work with translations.
You may even see the term "translational vector" used.
Consider this re-definition of the word "translation" using the term "vector".
 |
A translation is a transformation along a vector such that the segment joining a point to its image has the same length as the vector and is parallel to the vector. |
|
"A translation displaces every point in the plane by the same distance, in the same direction,
and can be described using a vector." NGMS
Keep in mind that the vector〈a, b〉is equivalent to the mapping (x, y) → (x + a, y + b).

Let's take a look at vectors in action!
Example 1: Given ΔABC and vector v.
Draw the translation determined by this vector and label the result ΔA'B'C'. |
Given:
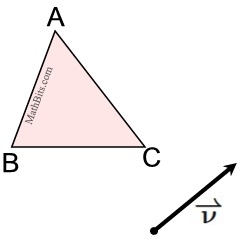 |
Result:
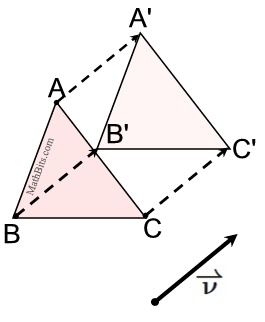 |
| Notice: all three "dashed" copies of the vector are all the SAME LENGTH as the given vector, and they are all PARALLEL to the given vector. |
| In this problem, you would need a compass and straightedge, or tracing paper to accurately draw the translated image. For construction directions, see Construct: Translations; |

| Keep in mind that the vector〈a, b〉is equivalent to the mapping (x, y) → (x + a, y + b). |
Example 2: Given ΔABC and vector v in the coordinate plane.
Draw the translation determined by this vector and label the result ΔA'B'C'. |
Given:
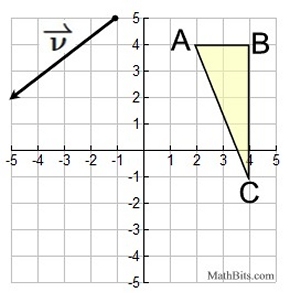 |
Result:
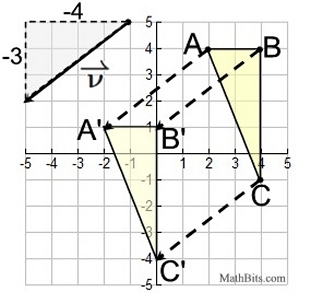
|
| Again, notice: all three "dashed" copies of the vector are all the SAME LENGTH as the given vector, and they are all PARALLEL to the given vector. |
Unlike the previous problem, no drawing tools are needed. Upon examination of the vector, it can be seen that movement by the vector is "left 4 units" and "down 3 units", written as 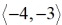 . These lengths can be easily applied on the coordinate grid to find the translation. . These lengths can be easily applied on the coordinate grid to find the translation. |

| Example 3: |
Given:
Given ABCD and vector: 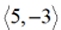
A(-3,5), B(-1,3). C(-3,1), D(-5,3)
Graph the pre-image and the image on the coordinate plane.
ABCD is graphed using the coordinates given.
The vector indicates a horizontal change of 5 units to the right, and
a vertical change of 3 units down.
A' (2,2), B' (4,0), C' (2,-2), D' (0,0)
|
Result:
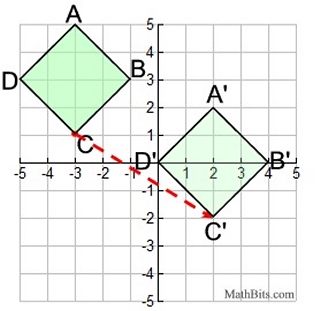
|
| The red dashed segment is showing the "translation vector". It is not needed in the answer. |

| Example 4: |
Given:
Given the graph shown below.
a) Which triangle is the pre-image and which triangle is the image? (pink vs blue)
b) What is the component form of the vector in this translation?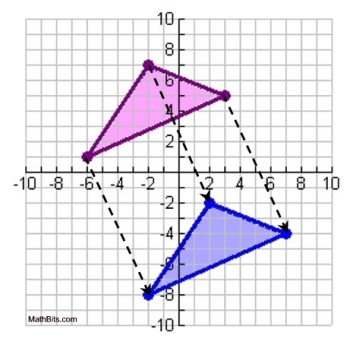 |
Result:
a) By observing that the arrowed segments are pointing to the blue triangle, we know that the blue triangle is the image, and the pink triangle is the pre-image.
b) the component form of the vector in this translation is
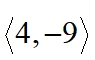
Notice that the vectors are all the same length and are parallel to one another.
|

 |
Two vectors:
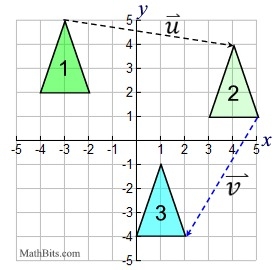 |
One vector:
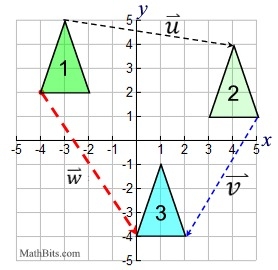
|
| A translation of a series of vectors can be accomplished in one step by adding the vectors. |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|