|
|
A cross section (or a plane section) is the intersection of a figure in three-dimensional space with a plane. A cross section is the face you obtain by making a "slice" through a solid object. A cross section is typically two-dimensional. |
|
We see cross sections in everyday life.
 A "slice" of bread.
A "slice" of bread.
Cross section: 
|
 A "slice" of cucumber.
Cross section: A "slice" of cucumber.
Cross section: 
|
 A "slice" of log.
A "slice" of log.
|

When a plane intersects a solid figure, the cross sectional face (or plane section) may be a point, a line segment, or a two-dimensional shape such as, but not limited to, a circle, rectangle, oval, or hexagon.
Point
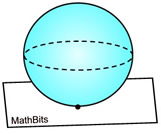
The plane is tangent to the sphere, intersecting in only one point.
|
Line Segment
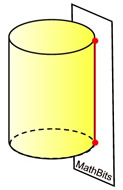 The plane is tangent to the side of the cylinder, intersecting in a line segment.
The plane is tangent to the side of the cylinder, intersecting in a line segment. |
Figure
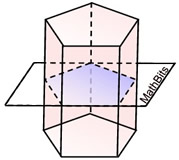 The plane cuts through the figure, intersecting in a pentagon. The plane may, or may not, be parallel to the base of the figure.
The plane cuts through the figure, intersecting in a pentagon. The plane may, or may not, be parallel to the base of the figure.
|

The figure (face) obtained from a cross section (plane section) depends upon
the orientation (angle) of the plane doing the cutting.
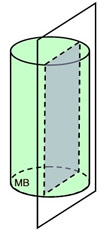
Right circular cylinder
Cross section:  rectangle rectangle
Plane orientation: perpendicular to the bases |
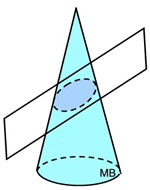
Right circular cone
Cross section: 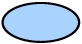 ellipse ellipse
Plane orientation: slanted (angled) across the cone |
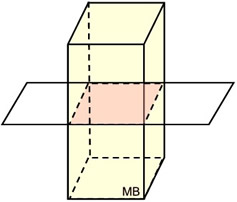
Right square prism
Cross section:
 square square
Plane orientation: parallel to the bases of the prism |

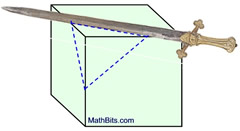
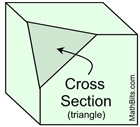
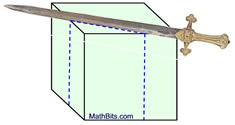
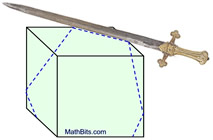
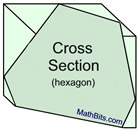
A single solid figure can be sliced to produce numerous cross sections of different forms.
In the diagrams below, the sword represents the "slicing" plane.
The solid object is a right rectangular prism.
The maximum number of "sides" of a cross section (plane section) equals the number of faces (surfaces) of the solid. Since the rectangular prism shown above has 6 faces, a cross section of that solid may have at most 6 sides. So a hexagon (6 sided) cross section is possible, but an octagon (8 sided) cross section is not possible. |

Note:  At this level, we are concentrating on slicing parallel or perpendicular to the base.
Additional slicings are mentioned for curricula that wish further examinations.. At this level, we are concentrating on slicing parallel or perpendicular to the base.
Additional slicings are mentioned for curricula that wish further examinations..
Slicing a Right Rectangular Prism |
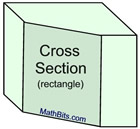
 Slice Parallel to the Base:
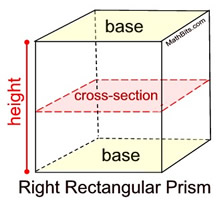
In a right rectangular prism, as seen at the right, all cross sections cut parallel to the base will be rectangles that are congruent to the base (that is, the same size and shape as the base). Slice Parallel to the Base:
In a right rectangular prism, as seen at the right, all cross sections cut parallel to the base will be rectangles that are congruent to the base (that is, the same size and shape as the base).
|
|
rc=
 Slice Perpendicular to Base: |
Option 1 - slice perpendicular to base, but parallel to a lateral side.
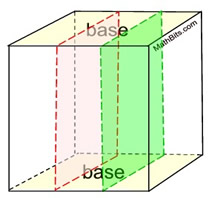
Right Rectangular Prism
In a right triangular prism, all cross sections cut perpendicular to the base, but parallel to a lateral side, will be rectangles that are congruent to that specific lateral side. |
Option 2 - slice perpendicular to base, but NOT parallel to a lateral side.
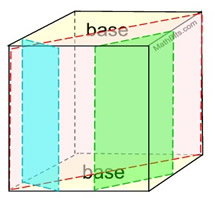
Right Rectangular Prism
In a right triangular prism, all cross sections cut perpendicular to the base, but NOT parallel to a lateral side, will be rectangles of varying sizes. |
Slice Slanted Across Figure:
In a right rectangular prism, as seen at the right, a cross sections can be cut on a slant to produce a variety of additional shapes. At the right, a slanted slice produced a triangle. Another slanted slice produced a trapezoid. A variety of 2-dimensional shapes are possible: triangles, quadrilaterals, pentagons and hexagons are possible.
We saw in the previous text that the cross section of a right rectangular prism can have at most 6 sides. So no octagons, etc.
|
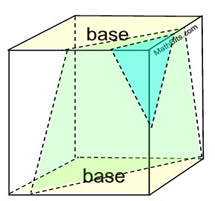 Right Rectangular Prism
Right Rectangular Prism
|

Slicing a Right Rectangular Pyramid |
 Slice Parallel to the Base: Slice Parallel to the Base:
In a right rectangular pyramid, as seen at the right, all cross sections cut parallel to the base will be rectangles that are similar to the base (that is, the same shape as the base, but not necessarily the same size).
|
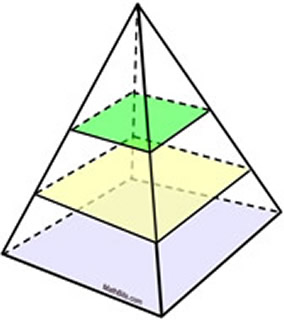 Right Rectangular Pyramid
Right Rectangular Pyramid
|
 Slice Perpendicular to Base: |
Option 1 - slice perpendicular to base, but parallel to a side of the base.
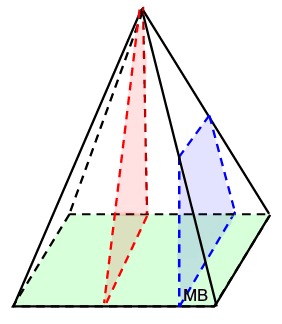
Right Rectangular Pyramid
In a right triangular pyramid, all cross sections cut perpendicular to the base, and also parallel to a side of the base, will be either a triangle, or a trapezoid of varying sizes. |
Option 2 - slice perpendicular to base, but NOT parallel to a side of the base.
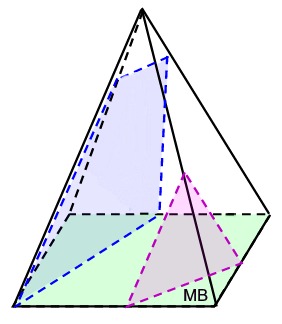
Right Rectangular Pyramid
In a right triangular pyramid, all cross sections cut perpendicular to the base, but NOT parallel to a side of the base, will also be either a triangles or a trapezoids of varying sizes. |
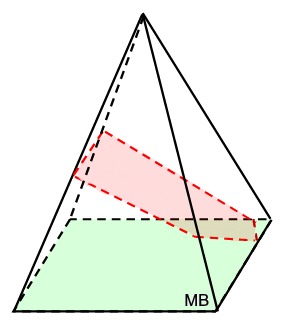
Slice Slanted Across Figure:
In a right rectangular pyramid, as seen at the right, a cross section can be cut on a slant to produce a variety of additional shapes.
At the right, a slanted slice produced a pentagon.
Remember, since a right rectangular pyramid has 5 faces, a cross section can have at most 5 sides.
So the cross sections for a right rectangular pyramid can be 2-dimensional shapes that are triangles, quadrilaterals, or pentagons.
|
 Right Rectangular Pyramid
Right Rectangular Pyramid
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|
|
|