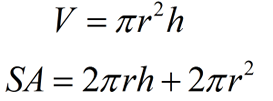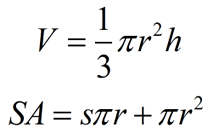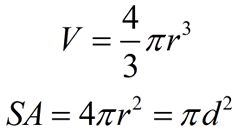Solids - Non Polyhedra MathBitsNotebook.com Topical Outline | JrMath Outline | MathBits' Teacher Resources Terms of Use   Contact Person: Donna Roberts

The study of three-dimensional (3D) space is called Solid Geometry.
A geometric solid (a 3-dimensional figure) is a portion of space which is completely enclosed, or separated from the rest of space, by some type of surface, or container.

A polyhedron (plural: polyhedra) is a three-dimensional solid made up of polygons.
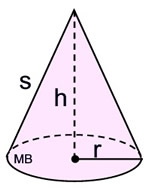
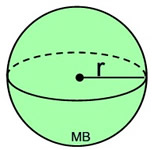
Polyhedra include prisms, pyramids and the Platonic Solids.
We worked with finding the surface area and volume of various polyhedra in past lessons.
A polyhedron has no curved surfaces.

Solids that have curved surfaces are classified as non-polyhedra
and include cylinders, cones and spheres.
These solids are not polyhedra since a part, or all, of the figure is curved.

Cylinder	Cone	Sphere

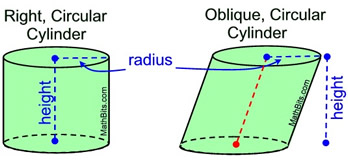
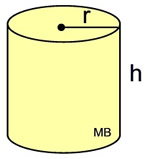
Designation: "Right"

In a manner similar to prisms and pyramids, the non-polyhedra we will be discussing are described as "right" cylinders or "right" cones. ("Right" has no meaning when discussing spheres.)

For a right cylinder, this means that the solid will appear to be upright (not slanted or looking like it may tip over) when sitting on its base (not "oblique"). That is, the bases will be directly above one another when it is sitting on its base. For a right cone, this means that the point (top, apex, vertex) of the cone will be directly over the center of the base (not slanted, nor leaning to the side).

Right versus Oblique Solids

Topical Outline | JrMath Outline | MathBitsNotebook.com | MathBits' Teacher Resources
Terms of Use    Contact Person: Donna Roberts