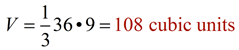|
Pyramids are three-dimensional closed surfaces.
At this level, the focus will be on right rectangular pyramids and right triangular pyramids.
|
A pyramid is a three-dimensional solid with one base, which is a polygon, and lateral faces that are triangles converging to a single point at the top (called the vertex, or apex). |
|
 Right Square Pyramid
Right Square Pyramid
|
Regarding right pyramids:
• |
The one and only base of the pyramid is a polygon
(no circles or ovals). |
• |
The lateral faces are always triangles with a common vertex. |
• |
The vertex of a pyramid (the point, the apex) is not in the same plane as the base. |
• |
Pyramids usually (but not always) sit on their bases. |
• |
All of the pyramids, at this level are right pyramids. |
• |
Pyramids are called polyhedra since their faces are polygons. |
|
Pyramids are named for the shapes of their bases.
 Triangular Base
Triangular Pyramid
Triangular Base
Triangular Pyramid |
 Square Base
Square Pyramid
Square Base
Square Pyramid |
 Hexagonal Base
Hexagonal Pyramid
Hexagonal Base
Hexagonal Pyramid |
|
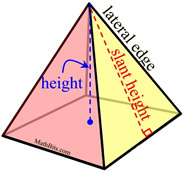
A right rectangular pyramid has a base that is a rectangle and lateral faces that are triangles. The height (altitude) is measured from the vertex (the top, apex) perpendicular to the base, intersecting at the center of the base. Slant height refers to the height (altitude) of each lateral face.
If the base is a square (that is, a regular polygon with all sides (and angles) of equal measure), then the 4 lateral triangles will be congruent to one another.
|
|
|
A right triangular pyramid has a base that is a triangle and e lateral faces that are also triangles. The height is measured in the same manner as in the right rectangular pyramid above.
If the base is an equilateral triangle, then the 3 lateral triangles will be congruent to one another (they may be isosceles or equilateral triangles). |
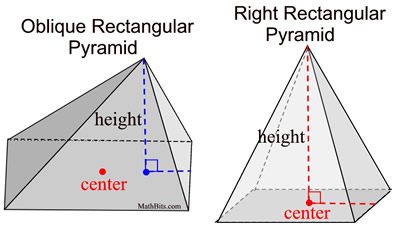
All pyramids discussed will be right pyramids.
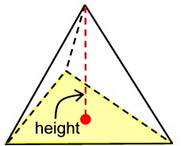
In a pyramid, that is a right pyramid, the altitude (height) is measured from the vertex perpendicular to base, where the intersection with the base is the center of the base. In a right, regular pyramid, the base is a regular polygon where all of the sides are of the same length.
FYI: Some pyramids can be "slanted" such that the height does not intersect with the center of the base.
These are called oblique pyramids. These will be studied in high school geometry.

Volume of a Pyramid:
The volume of a pyramid is one-third
the area of its base times its height.
B = base of pyramid, h = height
|
|
|
We know that V = Bh is the formula for the volume of a prism. By examining the formula of a pyramid, we could state that the volume of a pyramid is exactly one third the volume of a prism with the same base and height.
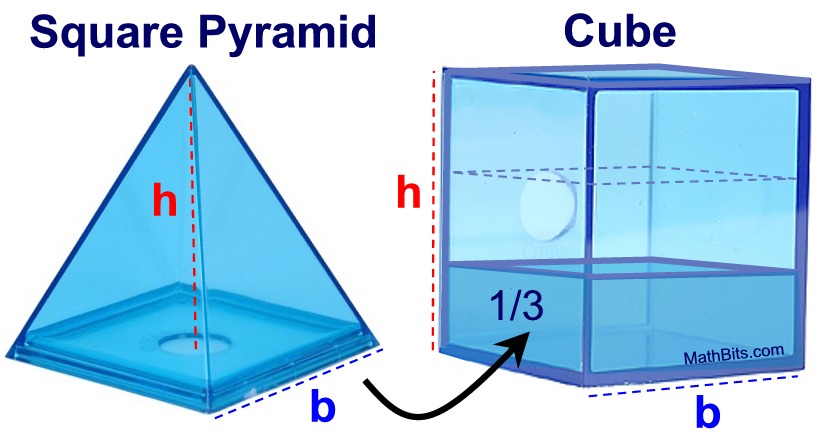
Justification of formula by "pour and measure":
(For this discussion, our pyramid will be a right square pyramid.)
We can conduct an experiment to demonstrate that the volume of a pyramid is actually equal to one-third the volume of a prism with the same base and height. We will fill a right square pyramid (whose height happens to be equal to the side of its base: b = h) with water. When the water is poured into a prism (a cube) with the same base and height as the pyramid, the water fills one-third of the prism (cube).
 |
| • |
The base of the pyramid is a square, with an area of b2. |
| • |
The base of the cube is a square, with
an area of b2. |
| • |
The height of the pyramid and the cube is h. |
| • |
In this example, b = h. |
|

The surface area of a pyramid is the sum of the area of the base plus the areas of the lateral faces. (The sum of the areas of all the faces.) |
|
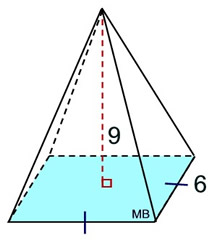
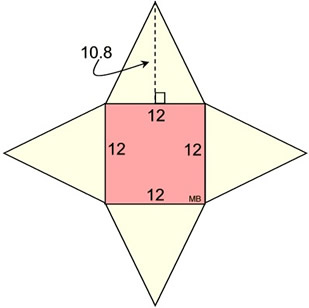
Example:
Find the surface area, SA, of this right, square pyramid. The slant height of the lateral side is 10.8 units.
|
|
Solution:
• Find the area of the base.
Since the base is a square, the A = s2.
A = 122 = 144 sq. units.
• Find the area of the triangular lateral faces. A = ½bh = ½ 12 • 10.8 = 64.8 sq. units
• Add the areas of all of the faces.
SA = 144 + 64.8 + 64.8 + 64.8 + 64.8
= 403.2 square units
The net on the right shows the faces of the pyramid that are used to find the surface area. |
 |
|

FYI: The work that was done in the example above can be combined to reveal
a "formula" for the surface area of a right pyramid.
B = area of the base
SA = 144 + 64.8 + 64.8 + 64.8 + 64.8
= 144 +
½ 12 • 10.8 + ½ 12 • 10.8 + ½ 12 • 10.8 + ½ 12 • 10.8
= 144 + ½ (48) • 10.8
= B + ½ (base perimeter)• slant height
The surface area, SA, of a right, regular pyramid can be found using the formula:
SA = B + ½ps
B = area of base, p = perimeter of base, s = slant height.
This is only for right regular pyramids where the
sides and angles of the polygonal base are of equal measure. |

|
A frustum is a portion of a solid (usually a pyramid or a cone) which remains after its upper part has been cut off by a plane parallel to its base. |
|
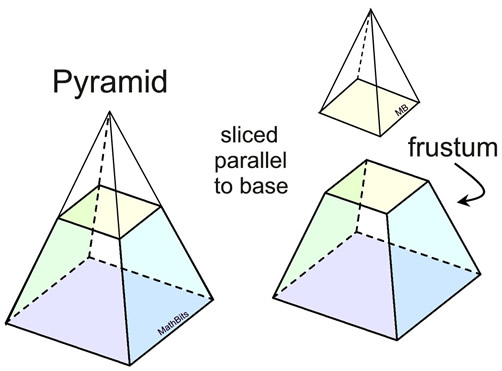
To find the volume of a frustum,
find the volume of the entire large pyramid
and subtract the volume of the smaller pyramid being cut off of the top.
The amount that remains, is the the volume of the frustum.
A frustum (in relation to pyramids) can also be called a truncated pyramid.
("truncated" means without its top or end section)

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|







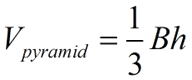

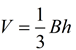 .
.