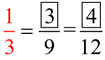|
In a scale drawing, you are dealing with objects of the same shape, but not necessarily the same size. As with similarity, the corresponding sides are proportional, with the ratios of their corresponding sides being equal.
The two rectangles shown at the right are similar.
But we can also think of these rectangles as a scale drawing with a scale factor.
Rectangle K is a scale drawing of rectangle B with a scale factor of 1:2. Every one inch of the scale drawing, K, represents 2 inches of initial rectangle B. |
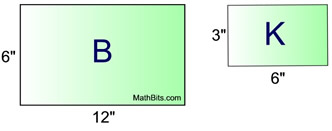 With K being the scale drawing of B,
With K being the scale drawing of B,
the scale factor is 1:2.
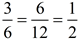
|
How do the areas of the rectangles compare?
The areas are NOT in the ratio of 1:2.
The areas are in a rato of 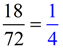 or 1:4 or 1:4
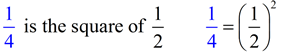 |
The area of rectangle B = 6 x 12 = 72 sq. in.
The area of rectangle K = 3 x 6 = 18 sq. in.
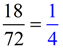 shows the ratio of the areas
to be the square of the scale factor of ½. |
|
If two polygons are similar, the ratio of their AREAS is equal to the SQUARE of the ratio of their corresponding sides (or the scale factor).
|
("corresponding sides" could be "sides", "altitudes", "diagonals", or "perimeters")

Triangle T is a scale drawing of triangle S with a scale factor of 3:5.
a) find the value of x.
b) If the height
in triangle T, drawn to base x, is 6 inches, find the height in triangle S, drawn to base of 15 in.
c) What is the ratio of the area of triangle T to the area of triangle S? 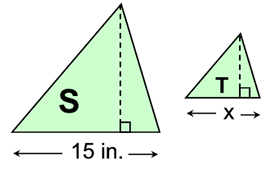 |
|


An architect's drawing shows a design which is actually 324 times larger than his drawing. If a measurement on the drawing is 2 inches, find the actual length, in feet, represented by that measurement.
|
Solution: The scale factor in inches is 1 : 324.
A length of 2 inches on the scale drawing will actually be 2(324) = 648 inches in length.
Convert inches to feet: (12 in. = 1 ft.)
648/12 = 54 feet. |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|


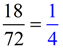 or
or 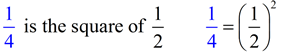


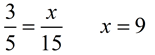
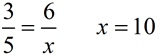
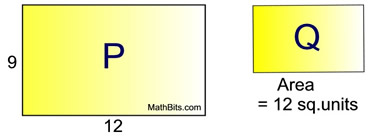
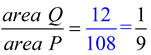 .
.