|
 Remember: area is labeled in square units: square inches, square feet, square meters, etc.
|
Area Formula
(Rectangle): |
A = l x w
l = length; w = width |
or A = bh
b = base; h = height |
|
|
Ways to recognize a rectangle:
|
Remember: in a triangle, the height must be drawn perpendicular (forming a right angle) to the base being used in the calculations.
Area Formula
(Triangle): |
A = ½ b • h or A = ½ bh
b = base; h = height drawn to that base |
|
|
 |
Types of
Triangles: |
 |
Acute Δ
 |
The height will make a right angle with the base.
Always be sure to use the height that is drawn TO the base you are using.
|
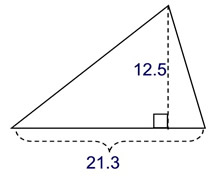
Find the area, in square units.
Solution: A = ½ b h = ½ (21.3)(12.5)
= 133.125 square units |
Right Δ
|
A right triangle will show a right angle at one vertex.
The legs of the right triangle become the "base" and the "height".
|
Find the area, in square units.
Solution: A = ½ b h = ½ (2½)(3¼)
|
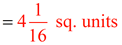
Equilateral Δ
|
Find x first using the area formula.
An equilateral triangle has all of its sides of equal length.
Perimeter is the distance around the outside.
|
Given: equilateral triangle shown
with an area of 40 square units
Find: perimeter of the triangle.
Solution: A = ½ bh; 40 = ½(x)(10)
40 = 5x, so x = 8. Each side = 8.
Perimeter = 3(8) = 24 units |
Obtuse Δ
|
Solution: A = ½ bh
= ½(8)(7)
= 28 sq. units
|
In an obtuse triangle, only one, of the three possible heights, can be drawn inside the triangle. The other two heights will lie outside the triangle.
The base side of the triangle needs to be extended to that it will intersect with its external height. |
Remember: While there is a formula for the area of a trapezoid, at this level, you will be asked to find the area by decomposing the trapezoid into triangles and rectangles.
|
Working with a
Trapezoid: |
decompose the trapezoid into triangles and rectangles when finding the area. |
|
|
|
 |
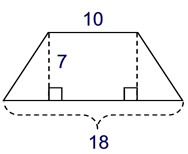In an isosceles trapezoid, the triangles on both sides will be of equal size.
To get the bases of the triangles, subtract 10 from 18, and divide by 2. |
Given: an isosceles trapezoid
Find: area by decomposing
Solution: the decomposition formed a rectangle and two right triangles.
Area of rectangle: A = bh = 10(7) = 70
Area of triangles: A= ½(4)(7) = 14 each
Area of trapezoid:
A
= 14 + 70 + 14 = 98 sq.units |
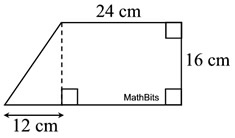
Given: figure above
Find: the area in sq.cm. |
This trapezoid is decomposed into a rectangle and a right triangle. |
Solution:
Area of rectangle: A = bh = 24(16) = 384
Area of triangle: A= ½(12)(16) = 96
Area of trapezoid:
A
= 384 + 96 = 480 sq.cm. |
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
