|
|
Volume is the amount of three-dimensional space an object occupies, in cubic units, within a container. |
|
In this section, we are going to be investigating how many small cubes (called unit cubes) can be placed inside of a right rectangular prism.
A connection will be made to the volume
of the right rectangular prism.
|
 |
Volume and Unit Cubes:
(in Right Rectangular Prisms) |
Volume is measured in cubic units. A "unit cube" with side lengths of one unit each, will have a volume of 1 cubic unit. If we can determine how many of these cubes will perfectly "fit" inside of a container, we will know the volume of the container, in cubic units.
So, the volume of an object can be represented by
the number of unit cubes that can be placed within the object.
|
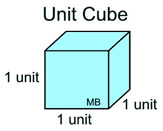 Volume = 1 cubic unit
Volume = 1 cubic unit |
Unit cubes are used when investigating the volume of right rectangular prisms (boxes).
To determine the volume, we can ask, "How many unit cubes can fit inside this box?"
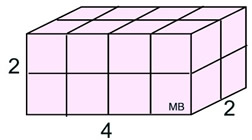 The dimensions of this box are
The dimensions of this box are
2 units by 4 units by 2 units. |
The volume of this right rectangular prism ("box") is the total of the number of unit cubes it holds.
By counting, we can see that there are are a total of 16 unit cubes within this solid.
The volume = 16 cubic units
Check: V = l x w x h = 2 x 4 x 2 = 16 |

For some figures, the unit cubes, with a volume of 1, fit "nicely" into the object,
while other objects may require fractional unit cubes.
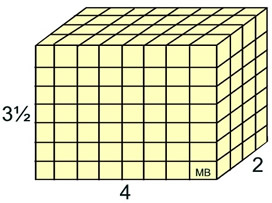
The dimensions of this box are
3½ units by 4 units by 2 units.
|
Because of the fractional side, 3½, the large box cannot be filled "exactly" with the unit cubes that have a volume of one. You cannot use half of a unit cube to finish filling the large box.
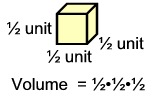
To deal with this problem, unit cubes with a with a side of ½ unit and a volume of 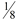 cubic units are needed. cubic units are needed.
The number of fractional cubes needed to fill the box is:
7 cubes x 8 cubes x 4 cubes = 224 cubes
BUT ... this is NOT the volume of the box |
.With this "new" fractional unit cube, the number of cubes used to fill the box, is NOT the volume of the box, as it was in the previous example. Each cube does not represent 1 cubic unit. Each cube now only represents 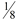 cubic units. We will need to multiply the number of cubes used by cubic units. We will need to multiply the number of cubes used by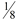 to get the actual volume of the big box ( 224 x to get the actual volume of the big box ( 224 x 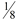 = 28 ). There are 28 cubic units in the big box. = 28 ). There are 28 cubic units in the big box.
Check: V = l x w x h = 3½ x 4 x 2 = 28 |

Volume as Area times Depth: |
While counting the number of unit cubes within the rectangular prism to determine volume,
a pattern can be seen that will help to determine the count of the cubes quickly.
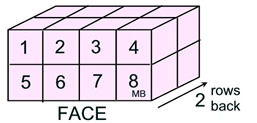
Pattern: Find the number of cubes seen in one face and multiply times the number of rows of that face, going to the back of the figure.
Volume = (cubes in face) • (rows going back)
= 8 • 2 = 16 square units |
|
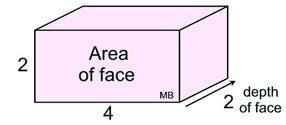
Pattern: A pattern similar to that shown above can be expressed using the term "area". The number of cube faces seen in the face of the figure, comprise the area of the face of the figure. The new pattern is expressed as:
Volume = (area of face) • (depth of face)
= (4 • 2) • 2 = 16 square units
|
|
 This pattern will be a popular strategy to determine the volume of many solids. This pattern will be a popular strategy to determine the volume of many solids.
• Flip the "box" over so it sits on its base.
• The area of the base is its length (l) times its width (w).
• Consider stacking copies of the area of the base (cross sections) on top of one another until they fill the solid.
•
This pattern utilizes what is called a "limiting argument" with the area being a 2-dimensional cross section with no thickness. • The thickness, however, can be theoretically considered very, very, very small so as not to affect calculations.
•
These cross sections are stacked
to the height (h) of the figure, creating the formula V = B • h, with B the area of the base and h = height. |
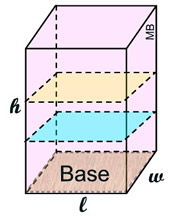
The area of the Base is l • w, call it B.
The volume of a "box" is V = l • w • h
Substitute B: V = B • h:
|
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|