Look for Hints in Problem
Read word problems carefully. This problem gives you the hint that volume is involved since it states "cubic inches". Also, the answer is for 100 die, not just one die.
EXAMPLE: A die (cube) has edges 0.62". A die mold holds 100 die. How many cubic inches, to the nearest cubic in, of liquid plastic is needed to fill this large mold?
Area cube = lwh or s3 = (0.62)3 cubic in.
For 100 cubes = 100 • (0.62)3
= 24 cubic inches |
|
Different Units of Measure
Read carefully to determine if all of the measurements within a problem are expressed in the same units. This example deals with inches, feet and yards.
EXAMPLE: A concrete truck holds 7.8 cubic yards of concrete. A patio being constructed is 18 feet across and 4 inches thick. How long, to nearest foot, is a patio constructed from the amount of concrete on the truck.
1 cubic yard = 27 cubic feet
7.8 × 27 = 210.6 cu. ft. on truck
4 in. is approximately 0.333 ft.
V = lwh
210.6 = (length)(18)(0.333)
Length 35 feet to nearest foot. |
|
Must Get Needed Information
When a formula needs a radius, be sure that you are working with the radius and not the diameter.
In this problem, the diameter is 12, but the radius is 6.
EXAMPLE:
Round to nearest cubic inch.
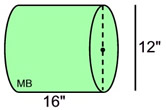 |
Find the volume.
V = πr2h = π(62)(16)
= 1810 cu.in. |
|
Use the Correct Formula
Especially when working with surface area, a formula may need to be adjusted to fit the situation.
EXAMPLE:
Round to nearest hundredth of a square inch.
 |
Find the surface area if this can has no lids.
SA = 2πrh = 2π(6)(16)
= 603.19 sq.in. |
The full formula for cylinder: SA = 2πrh + 2πr2
To remove the 2 lids (circles), remove 2πr2. |
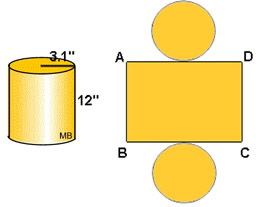
Consider Visualization
When dealing with surface area, it may be helpful to imagine the figure cut apart (called a net). In the example at the right, the top and bottom of the cylinder are cut off and the remaining center is flattened.
• AB = 12" the height of cylinder
• AD = circumference = 2πr = 19.48"
• Surface area = SA = 2πrh + 2πr2
= 2π(3.1)(12) + 2π(3.1)2 = 294.12 sq.in.
You can see that the area of the net is the area of the rectangle plus the area of the two circles. |
EXAMPLE: For this cylinder, find AB, AD, and the surface area of the cylinder.
Round to nearest hundredths.
 |
