Before we begin, let's remember the primary rule for working with linear inequalities:
... when you multiply (or divide) an inequality by a negative value,
you must change the direction of the inequality.

Now, let's see what happens when inequalities work in conjunction
(together) with one another.
A compound inequality is two simple inequalities joined by "and" or "or".
Compound Inequalities : OR |
|
|
Find the values for x which satisfy:
2x + 3 < 7 or 5x + 5 > 25
Solve each inequality separately.
Combine the results using the word "or".
Solve first inequality:
2x + 3 < 7
2x < 4
x < 2 |
Solve second inequality:
5x + 5 > 25
5x > 20
x > 4 |
The solution is x < 2 or x > 4.
Interval notation: 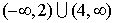
 |
The combined shaded regions on the number line represent numbers that are solutions of either x < 2 or x > 4 (or both if possible). These combined regions are referred to as the union of the two inequalities.
|
Example 1:
Solve for a: a - 5 > 0 or 3a - 1 < 8
a - 5 > 0
a > 5
|
3a - 1 < 8
3a < 9
a < 3 |
The solution is a < 3 or a > 5.
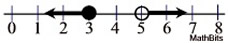
|
The answer is all real numbers that are less than or equal to 3 OR greater than 5. |
Example 2:
Write a compound inequality shown by this graph:
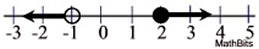
Let variable = x
The left side:
x < -1 |
The right side:
x > 2
|
The solution is:
x < -1 or x > 2
|
This problem is OR as the graphs do not overlap. |

Compound Inequalities : AND |
|
|
Find the values for x which satisfy:
8 < 3x - 1 and 4x + 2 < 22
Solve each inequality separately.
Combine the results using "and".
Look for where the solutions overlap.
Solve first inequality:
8 < 3x - 1
9 < 3x
3 < x |
Solve second inequality:
4x + 2 < 22
4x < 20
x < 5 |
The solution is x > 3 and x < 5.
Can also be written as: 3 < x < 5
Interval notation: (3, 5)
 |
When working with AND, you are looking for an overlapping region. You are looking for the numbers that are solutions for BOTH x < 3 and x > 5 at the same time. This overlapping region is referred to as the intersection of the two inequalities.
|
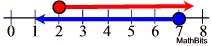
Example 3:
Solve for a: 3a - 9 < 12 and 3a - 9 > -3
3a - 9 < 12
3a < 21
a < 7
|
3a - 9 > -3
3a > 6
a > 2 |
The solution is a < 7 and a > 2.
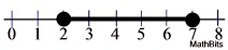
|
Answer is the overlapping of the two inequalities.
 |
Example 4:
Solve for x: -10 < 2x + 4 < 30
This solution can be approached in two ways.
1) You can deal with it as it appears and solve through the inequalities at the same time.
2) You can separate the problem into two parts and solve each part separately.
Either way, you will arrive at the same answer.
Method 1:
-10 < 2x + 4 < 30
subtract 4 from all sections
-14 < 2x < 26
divide all section by 2
-7 < x < 13
|
Method 2:
-10 < 2x + 4 and 2x + 4 < 30
-14 < 2x 2x < 26
-7 < x x < 13
-7 < x and x < 13
|
Example 5:
The antifreeze added to your car's cooling system claims that it will protect your car to -35º C and 120º C. The coolant will remain in a liquid state as long as the temperature in Celsius satisfies the inequality
-35º < C < 120º. Write this inequality in degrees Fahrenheit.
|
Remember:
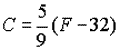
Plan:
-- set up inequality
-- substitute for C
-- solve for (isolate) F
|
|
Solution: The coolant will remain in a liquid state as long as the temperature in Fahrenheit degrees satisfies the inequality
-31º < F < 248º |